1)Cho hình vuông ABCD có cạnh dài 10 cm.Lấy điểm M trên cạnh AB sao cho AM=4 cm.
a)Tính diện tích tam giác MAD.
b)Gọi I là điểm chính giữa đoạn DM.Tính diện tích tam giác BIC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C2 :
Gọi số cần tìm là A ( A thuộc N )
Theo đề ta có :
A : 3 dư 1
A : 5 dư 1
A : 7 dư 1
\(\Rightarrow\left(A-1\right)⋮3⋮5⋮7\)
\(\Rightarrow A-1\in BC\left(3;5;7\right)=\left\{105;210;315;...;840;945;...\right\}\)
Mà A là STN lớn nhất có 3 chữ số
\(\Rightarrow A-1=945\)
\(\Rightarrow A=946\)

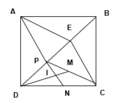
Vẽ hình đúng
a) Tính đúng diện tích hình vuông ABCD
b)-Lập luận đúng diện tích các tam giác ADP, APE, AEB, CPD, CPE, CEB bằng nhau và bằng 1 6 diện tích hình vuông ABCD.
-Lập luận được diện tích hình AECP bằng 1 3 diện tích hình vuông ABCD
-Tính đúng kết quả 12cm2
c)- Lập luận đúng diện tích tam giác DPM và DPN bằng nhau
- Lập luận đúng diện tích tam giác PMI và DNI bằng nhau

#novectorpicture
a)
Diện tích hình vuông ABCD là:
\(6\times6=36\left(cm^2\right)\)
b)
_Ta có:
\(S_{\Delta ADP}=S_{\Delta APE}=S_{\Delta AEB}=S_{\Delta CPD}=S_{\Delta CPE}=S_{\Delta CEB}=\frac{1}{3}S_{ABCD}\)(do các tam giác có cùng chiều cao và các đáy bằng nhau: BE = EP = PD)
_Lại có:
\(S_{AECP}=\frac{1}{3}S_{ABCD}\)
\(\Rightarrow S_{AECP}\)là:
\(\frac{1}{3}\times36=12\left(cm^2\right)\)
c)
_\(S_{\Delta DPM}=S_{\Delta DPN}=\frac{1}{2}S_{\Delta DPC}\)(do \(\Delta DPM\)và \(\Delta DPC\)có cùng chiều cao và \(MP=\frac{1}{2}PC\); \(ND=\frac{1}{2}DC\))
_\(S_{\Delta DPM}=S_{\Delta DPN}\)và đều có chung \(\Delta IPD\)
\(\Rightarrow S_{\Delta PMI}=S_{\Delta DNT}\)
Đáp số:....

Độ dài đoạn thẳng AE là :
10 : 2 = 5 (cm)
a) Diện tích hình thang BHDA là :
(10 + 5) x 10 : 2 = 75 (cm2)
b) Diện tích tam giác AHD:
10 x 10 : 2 = 50 (cm2)
Diện tích tam giác AHE:
5 x 5 : 2 =12.5 (cm2)
a) Vì H là trung điểm của BC nên BH==CH=1/2=12BC.
Độ dài đoạn thẳng BH và CH là:
10×1/2=5(cm)
Hình thang BHDA có đáy bé BH=5cm=5cm.
Diện tích hình thang BHDA là:
(10+5)×10:2=75(cm2)
Hình tam giác ABH có đáy BH=5cm
b) Diện tích hình tam giác ABH là:
10×5:2=25(cm2)
Ta có E là trung điểm của AB nên ta suy ra AE==BE=1/2=1/2AB.
Do AE=1/2=1/2AB với E nối liền với H và EH là một cạnh của hình tam giác AHE nên diện tích AHE=1/2=1/2 diện tích hình tam giác ABH.
Diện tích hình tam giác AHE là:
25×1/2=25/2(cm2)
Hình tam giác AHD có đáy AD=10cm
Diện tích hình tam giác AHD là:
10×10:2=50(cm2)
Đáp số: a)a) Diện tích hình thang BHDA bằng 75cm2
b)b) Diện tích hình tam giác AHE bằng 25/2cm2
Diện tích hình tam giác AHD bằng 50cm2
hok tốt

a: \(S_{BNDA}=\dfrac{1}{2}\cdot\left(BN+AD\right)\cdot AB=\dfrac{1}{2}\cdot20\cdot\left(10+20\right)=30\cdot10=300\left(cm^2\right)\)
b: Xét ΔMAD vuông tại A và ΔNBA vuông tại B có
MA=NB
AD=BA
=>ΔMAD=ΔNBA
=>góc AMD=góc BNA
=>góc DAN+góc ADM=90 độ
=>DM vuông góc AN
Vì AM<AD nên MO<DO
\(S_{ADN}=\dfrac{1}{2}\cdot DO\cdot AN;S_{AMN}=\dfrac{1}{2}\cdot MO\cdot AN\)
mà DO>MO
nên \(S_{ADN}>S_{AMN}\)
=>\(S_{DON}>S_{MON}\)

Mk nghĩ bn viết đề bài sai rùi, bn đã cho biết P ở đâu đâu mà đã cho BE=ED=PD
Bài 1:x*(x+1)=132
=>x2+x=132
=>x2+x-132=0
=>x2+
=>(x+12)(x-11)=0
sr máy mk ko hiểu tại sao chuột nó tự lên lại xuống nên mk bấm nhầm
Bài 1:x*(x+1)=132
=>x2+x=132
=>x2+x-132=0
=>x2-11x+12x-132=0
=>x(x-11)+12(x-11)=0
=>(x+12)(x-11)=0
=>x+12=0 hoặc x-11=0
=>x=-12 hoặc x=11