Tìm a để phương trình 2x - 5a +3 =0 và phương trình 2x +4 = 0 tương đương với nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
26 tháng 2 2020
1) Ta có : \(mx^2-\left(m+1\right)x+1=\left(x-1\right)\left(2x-1\right)\)
\(\Leftrightarrow mx^2-\left(m+1\right)x+1=2x^2-3x+1\)
Đồng nhất hệ số \(\Rightarrow\hept{\begin{cases}m=2\\m+1=3\end{cases}\Rightarrow m=2}\)
2) Ta có \(\left(x-3\right)\left(ax+2\right)=\left(2x+b\right)\left(x+1\right)\)
\(\Leftrightarrow ax^2+\left(2-3a\right)x-6=2x^2+x\left(2+b\right)+b\)
Đồng nhất hệ số \(\Rightarrow\hept{\begin{cases}a=2\\2-3a=2+b\\-6=b\end{cases}\Rightarrow}\hept{\begin{cases}a=2\\b=-6\end{cases}}\)
HP
4 tháng 5 2021
b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
HP
4 tháng 5 2021
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)
TT
4 tháng 3 2020
a) Ta có :
\(3x=3\left(x+2\right)\)
\(\Leftrightarrow3x=3x+2\)
\(\Leftrightarrow0=2\) ( vô lí )
Do đó pt đã cho vô nghiệm
b) Ta có \(\left|x\right|=-x^2-2\) (1)
Nhân xét : VT (1) : \(\left|x\right|\ge0\forall x\)
VP (1) : \(-x^2\le0\Leftrightarrow-x^2-2\le-2\forall x\)
Do đó : \(VT\ne VP\)
Vì vậy pt đã cho vô nghiệm
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 8 2021
Đặt \(\sqrt{-x^2+2x+15}=t\Rightarrow0\le t\le4\)
BPT trở thành:
\(-4t\ge-t^2+2+m\)
\(\Leftrightarrow t^2-4t-2\ge m\)
\(\Rightarrow m\le\min\limits_{\left[0;4\right]}\left(t^2-4t-2\right)\)
Xét \(f\left(t\right)=t^2-4t-2\) trên \(\left[0;4\right]\)
\(-\dfrac{b}{2a}=2\in\left[0;4\right]\)
\(f\left(0\right)=f\left(4\right)=-2\) ; \(f\left(2\right)=-6\)
\(\Rightarrow f\left(t\right)_{min}=-6\Rightarrow m\le-6\)
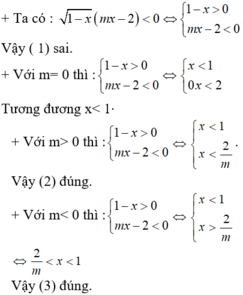
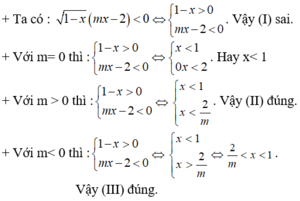
Đầu tiên b hãy cho nó tương đươnng nhé:
2x-5a+3=2x+4
<=>2x-2x-5a=4-3
<=>-5a=1<=>a=-1/5