Bài 5. Cho hình vẽ sau, biết BD =2/3 BC và
DE = 1/3 AD và diện tích tam giác ABE
bằng 24cm2. Tính diện tích tam giác ABC
MÌNH ĐANG CẦN RẤT GẤP, TRL NHANH GIÚP MK ĐC KO???
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2
Ta có: AE+ED=AD
=>\(AE+\dfrac{1}{3}AD=AD\)
=>\(AE=\dfrac{2}{3}AD\)
=>\(S_{ABE}=\dfrac{2}{3}\cdot S_{ABD}\)
=>\(S_{ABD}=\dfrac{3}{2}\cdot24=36\left(cm^2\right)\)
Vì \(BD=\dfrac{2}{3}BC\)
nên \(S_{ABD}=\dfrac{2}{3}\cdot S_{ABC}\)
=>\(S_{ABC}=36\cdot\dfrac{3}{2}=54\left(cm^2\right)\)
CM
18 tháng 8 2018
Vì BD =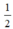 
DC nên diện tích tam giác ABD = 
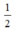diện tích tam giác ADC (do hai tam giác có cùng chiều cao)
Diện tích tam giác ADC là:
24 x 2 = 48 (cm2)
Diện tích tam giác ABC là:
24 + 48 = 72 (cm2)
Đáp số: 72 cm2.
6 tháng 1 2016
Vì BD=1/2DC nên BD=1/3 AC . Suy rA ABD=1/3 ABC =>ABC=72(cm2)
\(S_{ABD}=\frac{2}{3}\times S_{ABC}\)(\(BD=\frac{2}{3}\times BC\), chung đường cao hạ từ \(A\))
\(S_{ABE}=\frac{2}{3}\times S_{ABD}\)(\(AE=\frac{2}{3}\times AD\), chung đường cao hạ từ \(B\))
suy ra \(S_{ABE}=\frac{2}{3}\times\frac{2}{3}\times S_{ABC}=\frac{4}{9}\times S_{ABC}\)
\(\Rightarrow S_{ABC}=\frac{9}{4}\times S_{ABE}=54\left(cm^2\right)\)