Bài 4: (3,5 đ) Cho tam giác ABC vuông tại A, phân giác BE. Kẻ EK vuông góc với BC tại K. Gọi M là giao điểm của BA và KE. Chứng minh :
a) ΔABE = ΔKBE
b) EM = EC
c) AK // MC mn ơi giúp em với tý em nộp r ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại A và ΔKBE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔABE=ΔKBE
b: Xét ΔAEM vuông tại A và ΔKEC vuông tại K có
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)
Do đó: ΔAEM=ΔKEC
Suy ra: EM=EC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC

a: Xét ΔBAE vuông tại A và ΔBKE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔBAE=ΔBKE
b: ta có: ΔBAE=ΔBKE
=>EA=EK
Xét ΔEAM vuông tại A và ΔEKC vuông tại K có
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)(hai góc đối đỉnh)
Do đó: ΔEAM=ΔEKC
=>EM=EC
c: Ta có: ΔEAM=ΔEKC
=>AM=KC
Ta có: ΔBAE=ΔBKE
=>BA=BK
Xét ΔBMC có \(\dfrac{BA}{AM}=\dfrac{BK}{KC}\)
nên AK//MC
d: Ta có: NM=NC
=>N nằm trên đường trung trực của MC(1)
Ta có: EM=EC
=>E nằm trên đường trung trực của CM(2)
Ta có: BA+AM=BM
BK+KC=BC
mà BA=BK và AM=KC
nên BM=BC
=>B nằm trên đường trung trực của MC(3)
Từ (1),(2),(3) suy ra B,E,N thẳng hàng

a: Xét ΔABE vuông tại A và ΔKBE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔABE=ΔKBE
b: Xét ΔAEM vuông tại A và ΔKEC vuông tại K cso
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)
Do đó:ΔAEM=ΔKEC
Suy ra: EM=EC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC

a: Xét ΔBAE vuông tại A và ΔBKE vuông tại K có
BE chung
góc ABE=góc KBE
=>ΔBAE=ΔBKE
b: Xét ΔEAM vuông tại A và ΔEKC vuông tại K có
EA=EK
góc AEM=góc KEC
=>ΔEAM=ΔEKC
=>EM=EC và AM=KC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC
d: BM=BC
Em=EC
=>BE là trung trực của MC
=>B,E,N thẳng hàng

Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
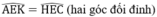
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)

a: Xét ΔABK vuông tại A và ΔEBK vuông tại E có
BK chung
\(\widehat{ABK}=\widehat{EBK}\)
Do đó: ΔABK=ΔEBK
b: Ta có: ΔABK=ΔEBK
nên KA=KE
c: Ta có: KA=KE
AB=EB
Do đó: BK là đường trung trực của AE
a) Xét tam giác BAK và tam giác BEK:
Góc A=góc E
Góc B1=B2
BK - cạch chung
Vậy tam giác BAK= tam giác BEK (cạch huyền góc nhọn)
b)Theo CMa)vì tam giác BAK= tam giác BEK
Vậy KA=KE (2 cạnh tương ứng)
c)Xét tam giác AKM và tam giác EKC
Góc K1= góc k2
Vì 2 góc A1 và A2 là 2 góc kề bù mà A1=90độ => A2=90 độ (1)
Góc E1 và E2 là 2 góc kề bù mà E1=90độ =>E2 =90 độ (2)
Từ (1) và (2) ta có: góc A2= góc E2 (=90 độ)
Vậy tam giác AKM= tam giác EKC (cạnh huyền góc vuông)
=> MK=KC (2 cạnh tương ứng

a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥⊥CK
tham khảo
a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥CK