Tìm GTNN của biểu thức sau:
B= 5x2 + x -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
ĐKXĐ: x<>0
\(B=\dfrac{-x^2-x-1}{x^2}\)
\(=-1-\dfrac{1}{x}-\dfrac{1}{x^2}\)
\(=-\left(\dfrac{1}{x^2}+\dfrac{1}{x}+1\right)\)
\(=-\left(\dfrac{1}{x^2}+2\cdot\dfrac{1}{x}\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^2-\dfrac{3}{4}< =-\dfrac{3}{4}\forall x< >0\)
Dấu '=' xảy ra khi 1/x+1/2=0
=>1/x=-1/2
=>x=-2

a: Ta có: \(A=2x^2-8x+1\)
\(=2\left(x^2-4x+\dfrac{1}{2}\right)\)
\(=2\left(x^2-4x+4-\dfrac{7}{2}\right)\)
\(=2\left(x-2\right)^2-7\ge-7\forall x\)
Dấu '=' xảy ra khi x=2

A=5x2+2y2−4xy−8x−4y+19=(2x2−4xy+2y2)+4(x−y)+(3x2−12x)+19=2(x−y)2+4(x−y)+3(x2−4x+4)+7=2[(x−y)2+2(x−y)+1]+3(x−2)

Ta có: \(B=-x^2-2x+2\)
\(\Rightarrow BMax\Leftrightarrow-x^2-2x+2Max\)
\(\Leftrightarrow-\left(x^2+2x-2\right)Max\)
\(\Leftrightarrow-\left(x^2+2x+1-3\right)Max\)
\(\Leftrightarrow-\left[\left(x+1\right)^2-3\right]Max\)
\(\Leftrightarrow-\left(x+1\right)^2+3Max\)
Vì \(-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+1\right)^2+3\le3\forall x\)
Dấu = xảy ra \(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
\(\Rightarrow MaxB=3\Leftrightarrow x=-1\)

Với \(x\ge\dfrac{1}{6}\Leftrightarrow A=5x^2-6x+1-1=5x^2-6x\)
\(A=5\left(x^2-2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{9}{5}=5\left(x-\dfrac{3}{5}\right)^2-\dfrac{9}{5}\ge-\dfrac{9}{5}\\ A_{min}=-\dfrac{9}{5}\Leftrightarrow x=\dfrac{3}{5}\left(1\right)\)
Với \(x< \dfrac{1}{6}\Leftrightarrow A=5x^2+6x-1-1=5x^2+6x-2\)
\(A=5\left(x^2+2\cdot\dfrac{3}{5}x+\dfrac{9}{25}\right)-\dfrac{19}{5}=5\left(x+\dfrac{3}{5}\right)^2-\dfrac{19}{5}\ge-\dfrac{19}{5}\\ A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow A_{min}=-\dfrac{19}{5}\Leftrightarrow x=-\dfrac{3}{5}\)
Với \(x\ge\dfrac{1}{3}\Leftrightarrow B=9x^2-6x-4\left(3x-1\right)+6=9x^2-18x+10\)
\(B=9\left(x^2-2x+1\right)+1=9\left(x-1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=1\left(1\right)\)
Với \(x< \dfrac{1}{3}\Leftrightarrow B=9x^2-6x+4\left(3x-1\right)+6=9x^2+6x+2\)
\(B=\left(9x^2+6x+1\right)+1=\left(3x+1\right)^2+1\ge1\\ B_{min}=1\Leftrightarrow x=-\dfrac{1}{3}\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrow B_{min}=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
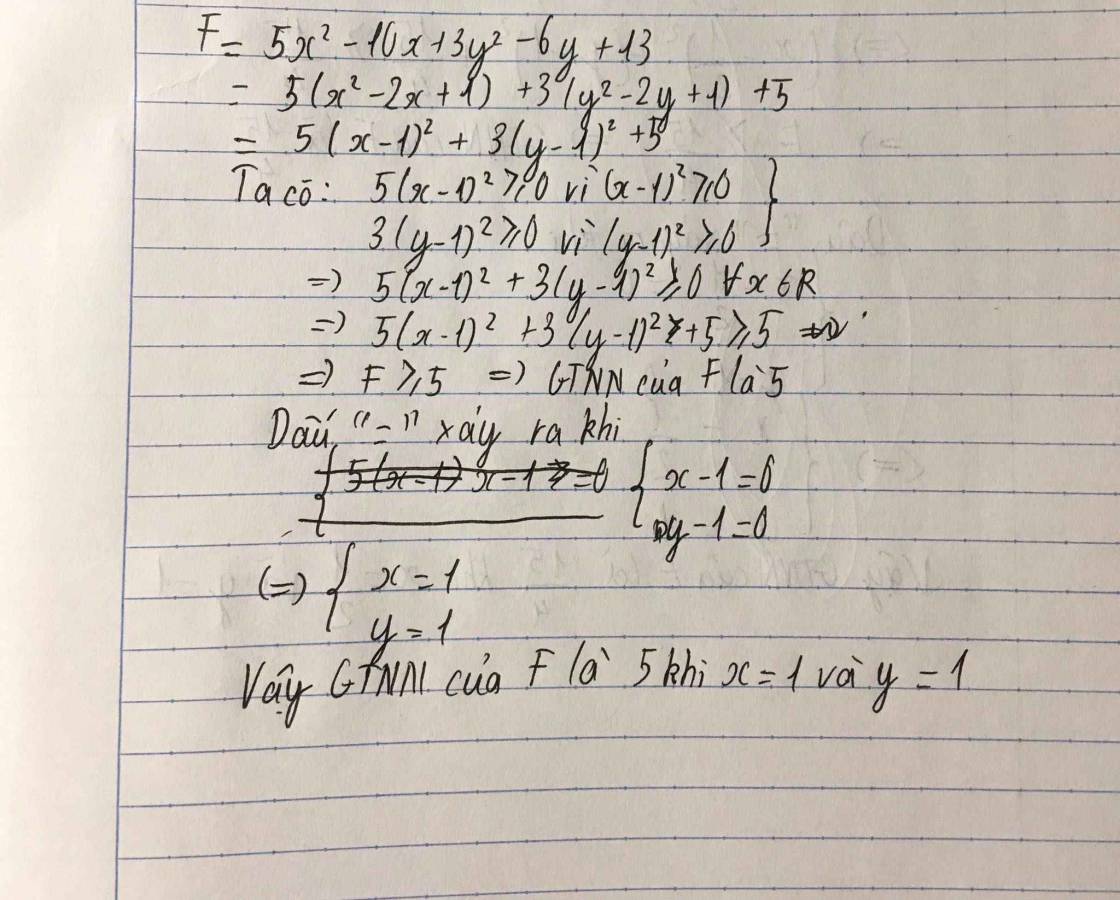
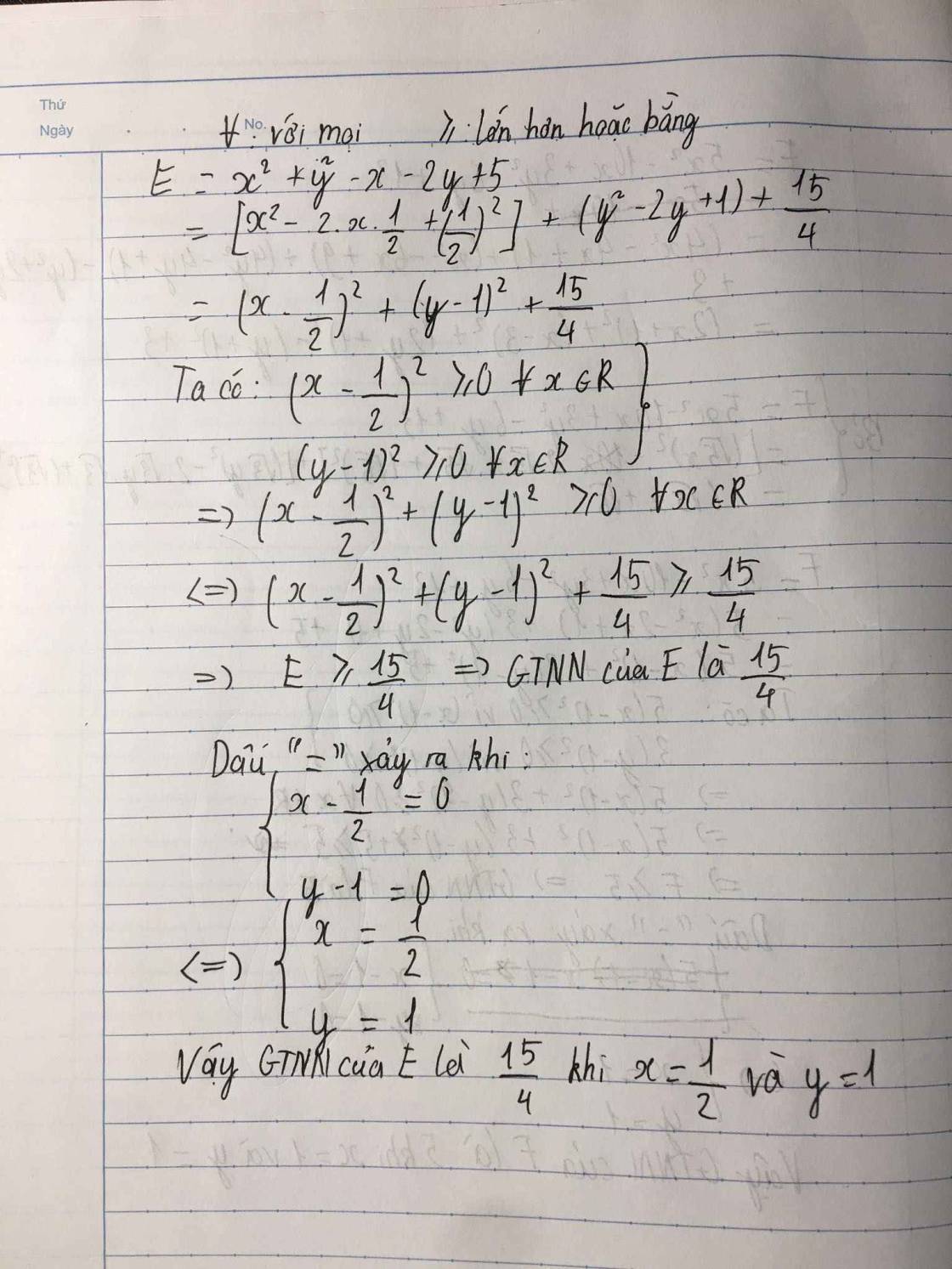
\(B=5x^2+x+1\)
\(=>5\left(x^2+\frac{1}{5}x+\frac{1}{5}\right)\)
\(=>5\left(x^2+2.x.\frac{1}{10}+\frac{1}{100}+\frac{19}{100}\right)\)
\(=>5\left(\left(x+\frac{1}{10}\right)^2+\frac{19}{100}\right)\)
\(=>\frac{19}{20}+5\left(x+\frac{1}{10}\right)^2\ge\frac{19}{20}\)
MIN B = \(\frac{19}{20}< =>x+\frac{1}{10}=0=>x=\frac{-1}{10}\)
B = 5x2 + x - 1
\(=5\left(x^2+\frac{1}{5}x-\frac{1}{5}\right)=5\left[x^2+2.\frac{1}{10}.x+\left(\frac{1}{10}\right)^2-\left(\frac{1}{10}\right)^2-\frac{1}{5}\right]\)
\(=5\left[\left(x+\frac{1}{10}\right)^2-\frac{21}{100}\right]=5\left(x+\frac{1}{10}\right)^2-\frac{21}{20}\ge-\frac{21}{20}\)
Vậy MinB = -21/20 khi \(x+\frac{1}{10}=0\Rightarrow x=-\frac{1}{10}\)