Cho tam giác ABC vuông tại A có AH là đường cao và độ dài cạnh huyền BC là 2a. Gọi D,E lần lượt là hình chiếu của H lên AB,AC. Tìm giá trị lớn nhất của độ dài cạnh DE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao
Theo hệ thức giữa đường cao và hình chiếu ta có:
A H 2 = HB.HC = 4.9 = 36 ⇒ AH = 6 (cm)
Vậy DE = 6 (cm)

Xét hai tam giác vuông ABH và CAH có:
∠ ABH = ∠ CAH (cùng phụ với góc ∠ BAH)
Do đó △ ABH đồng dạng △ CAH (g.g).
Suy ra: 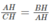
⇒ A H 2 = BH. CH = 4.9 = 36 ⇒ AH = 6(cm)
Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.
Suy ra: DE = AH = 6 (cm)

Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)

a: Xét tứ giác ADME có
gócADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: góc AHM=góc AEM=góc ADM=90 độ
=>A,D,H,M,E cùng thuộc đường tròn đường kính AM
mà ED và AM cùng là đường kính của đường tròn đường kính AM(ED=AM)
nên H nằm trên đường tròn đường kính DE
=>góc DHE=90 độ
c: DE=AM
AM>=AH
=>DE>=AH
Dấu = xảy ra khi M trùng với H
=>M là chân đường cao kẻ từ A xuống BC
Ta thấy ngay DE = AH do EHDA là hình chữ nhật.
Gọi độ dài hai cạnh góc vuông lần lượt là x và y, khi đó ta có: \(AH=\frac{xy}{2a}\le\frac{x^2+y^2}{4a}=\frac{4a^2}{4a}=a\)
Vậy độ dài lớn nhất của DE là a, khi tam giác ABC vuông cân tại A.