giúp tôi 3(x-1)ngũ 2- 3(x-5)=1
cho tôi đáp án nhanh nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8-4 : 3/4 =8-13/4
3/7:3/5 -4/7 =5/7-4/7=1/7
5/8 x 2/5 + 5/8 x3/5 =5/8 x (2/5+3/5)=5/8 x 1=5/8
$#flo2k9$
`8 - 4 : 3/4 = 8 - 4 xx 4/3 = 8 - 16/3 = 8/3`
`3/7 : 3/5 - 4/7 = 3/7 xx 5/3 - 4/7 = 5/7 - 4/7 = 1/7`
`5/8 xx 2/5 + 5/8 xx 3/5 = 5/8 xx ( 2/5 + 3/5) = 5/8 xx 1= 5/8`

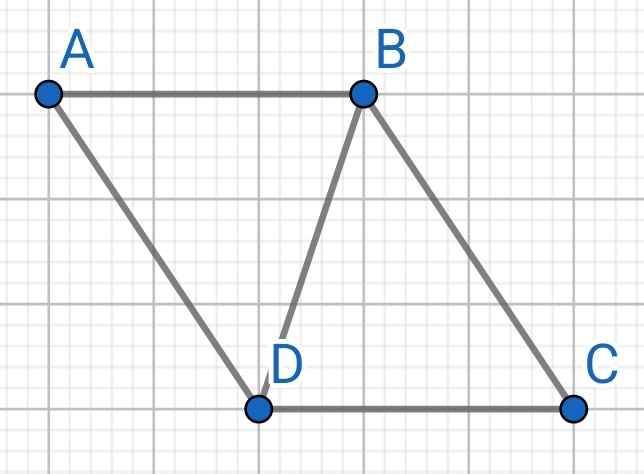 Do AB // CD (gt)
Do AB // CD (gt)
⇒ ∠ABD = ∠CDB (so le trong)
Xét ∆ABD và ∆CDB có:
AB = CD (gt)
∠ABD = ∠CDB (cmt)
BD chung
⇒ ∆ABD = ∆CDB (c-g-c)
⇒ AD = BC (hai cạnh tương ứng)
Do ∆ABD = ∆CDB (cmt)
⇒ ∠ADB = ∠CBD (hai góc tương ứng)
Mà ∠ADB và ∠CBD là hai góc so le trong
⇒ AD // BC

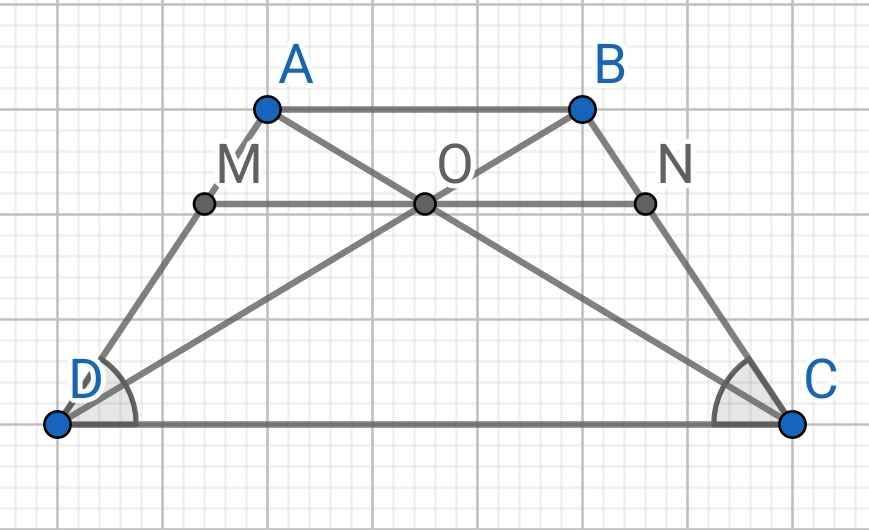 a) Do ABCD là hình thang cân
a) Do ABCD là hình thang cân
⇒ AD = BC (hai cạnh bên)
∠ADC = ∠BCD (hai góc kề đáy CD)
Xét ∆ADC và ∆BCD có:
AD = BC (cmt)
∠ADC = ∠BCD (cmt)
CD chung
⇒ ∆ADC = ∆BCD (c-g-c)
⇒ ∠ACD = ∠BDC (hai góc tương ứng)
b) Do MN // AB // CD
⇒ ON // AB // CD
Do CD // ON (cmt)
⇒ ∠ACD = ∠NOC (so le trong)
Do CD // AB (gt)
⇒ ∠BDC = ∠ABD (so le trong)
Do AB // ON (cmt)
⇒ ∠ABD = ∠BON (so le trong)
c) Do ∠ACD = ∠NOC (cmt)
∠ACD = ∠BDC (cmt)
⇒ ∠NOC = ∠BDC
Mà ∠BDC = ∠ABD (cmt)
⇒ ∠NOC = ∠ABD
Lại có ∠ABD = ∠BON (cmt)
⇒ ∠NOC = ∠BON
Vậy ON là tia phân giác của ∠BOC

a) \(16x^2-1\)
\(=\left(4x\right)^2-1^2\)
\(=\left(4x-1\right)\left(4x+1\right)\)
b) \(\left(x+2\right)^2-49y^2\)
\(=\left(x+2\right)^{^2}-\left(7y\right)^2\)
\(=\left[\left(x+2\right)-7y\right]\left[\left(x+2\right)+7y\right]\)
\(=\left(x+2-7y\right)\left(x+2+7y\right)\)
c) \(4x^2-12xy+9y^2\)
\(=\left(2x\right)^2-2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=\left(2x-3y\right)^2\)
d) \(\left(a+b\right)^2-\left(2a-b\right)^2\)
\(=\left[\left(a+b\right)+\left(2a-b\right)\right]\left[\left(a+b\right)-\left(2a-b\right)\right]\)
\(=\left(a+b+2a-b\right)\left(a+b-2a+b\right)\)
\(=3a\cdot\left(2b-a\right)\)
e) \(\left(x-y\right)^2-2\left(x-y\right)z+z^2\)
\(=\left[\left(x-y\right)-z\right]^2\)
\(=\left(x-y-z\right)^2\)
g) \(-3x^2+6xy-3y^2\)
\(=-\left(3x^2-6xy+3y^2\right)\)
\(=-3\left(x^2-2xy+y^2\right)\)
\(=-3\left(x-y\right)^2\)
a: 16x^2-1=(4x)^2-1=(4x-1)(4x+1)
b: (x+2)^2-49y^2
=(x+2)^2-(7y)^2
=(x+2+7y)(x+2-7y)
c: 4x^2-12xy+9y^2=(2x-3y)^2
d: (a+b)^2-(2a-b)^2
=(a+b+2a-b)(a+b-2a+b)
=(2b-a)*3a
g: =-3(x^2-2xy+y^2)
=-3(x-y)^2

\(a,6a^2b+9ab^2\)
\(=3ab\left(2a+3b\right)\)
\(b,5x^3y^2-15x^2y^3\)
\(=5x^2y^2\left(x-3y\right)\)
\(c,2x\left(x+1\right)-3y\left(x+1\right)\)
\(=\left(x+1\right)\left(2x-3y\right)\)
\(d,\left(x-y\right)^2-x\left(x-y\right)\)
\(=\left(x-y\right)\left(x-y-x\right)\)
\(=-y\left(x-y\right)\)
\(e,y\left(x-1\right)-x\left(1-x\right)\)
\(=y\left(x-1\right)+x\left(x-1\right)\)
\(=\left(x-1\right)\left(y+x\right)\)
\(g,2a\left(a-b\right)+2b\left(b-a\right)\)
\(=2a\left(a-b\right)-2b\left(a-b\right)\)
\(=\left(2a-2b\right)\left(a-b\right)\)
\(=2\left(a-b\right)^2\)
#Urushi☕
a: 6a^2b+9ab^2
=3ab*2a+3ab*3b
=3ab(2a+3b)
b: 5x^3y^2-15x^2y^3
=5x^2y^2*x-5x^2y^2*3y
=5x^2y^2(x-3y)
c: 2x(x+1)-3y(x+1)
=(x+1)(2x-3y)
d: =(x-y)(x-y-x)
=-y(x-y)
e: =y(x-1)+x(x-1)
=(x-1)(x+y)
g: =2a(a-b)-2b(a-b)
=(a-b)(2a-2b)
=2(a-b)^2

1: Xét tứ giác ABEC có
AB//EC
AC//BE
=>ABEC là hình bình hành
=>BE=AC
mà AC=BD
nên BE=BD
2:
ΔBED cân tại B
mà BH là đường cao
nên H là trung điểm của DE
3: Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
=>góc OAB=góc OBA
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD

b. \(2x=\dfrac{-1}{5}\)
\(x=-0,25\)
d. \(\dfrac{2}{x+1}=\dfrac{x+1}{16}\)
\(\Leftrightarrow\left(x+1\right)^2=32\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=4\sqrt{2}\\x+1=-4\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\sqrt{2}-1\\x=-4\sqrt{2}-1\end{matrix}\right.\)