Giải phương trình: x4+x3+x+1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
19 tháng 1 2019
Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
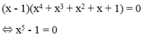
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.
PT
1
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
PT
1
15 tháng 12 2021
Đặt x2−2x+m=tx2−2x+m=t, phương trình trở thành t2−2t+m=xt2−2t+m=x
Ta có hệ {x2−2x+m=tt2−2t+m=x{x2−2x+m=tt2−2t+m=x
⇒(x−t)(x+t−1)=0⇒(x−t)(x+t−1)=0
⇔[x=tx=1−t⇔[x=tx=1−t
⇔[x=x2−2x+mx=1−x2+2x−m⇔[x=x2−2x+mx=1−x2+2x−m
⇔[m=−x2+3xm=−x2+x+1⇔[m=−x2+3xm=−x2+x+1
Phương trình hoành độ giao điểm của y=−x2+x+1y=−x2+x+1 và y=−x2+3xy=−x2+3x:
−x2+x+1=−x2+3x−x2+x+1=−x2+3x
⇔x=12⇒y=54⇔x=12⇒y=54
Đồ thị hàm số y=−x2+3xy=−x2+3x và y=−x2+x+1y=−x2+x+1:
PT
1
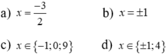
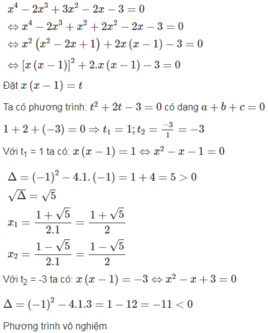
(x^4+ x^3) + x +1=0
=> x^3 (x+1) +x+1 =0
=>( x^3+1)(x+1)=0
=> \(\orbr{\begin{cases}x^3+1=0\\x+1=0\end{cases}}< =>x=-1\)
Vay S ={-1}
\(x^4+x^3+x+1=0\)
\(\Leftrightarrow\left(x^4+x\right)+\left(x^3+1\right)=0\)
\(\Leftrightarrow x\left(x^3+1\right)+\left(x^3+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+1\right)\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+1\right)^2=0\\x^2-x+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x+1=0\\\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-1\\\left(x-\frac{1}{2}\right)^2=-\frac{3}{4}\left(vn\right)\end{cases}}\Leftrightarrow x=-1\)
vn : vô nghiệm.
Vậy phương trình có nghiệm duy nhất : \(x=-1\)