so sánh máy tính AOC và máy tính samsung
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
AH
Akai Haruma
Giáo viên
7 tháng 8 2021
Lời giải:
$\sqrt{15}< \sqrt{16}=4$
$\sqrt{17}< \sqrt{25}=5$
$\Rightarrow \sqrt{15}+\sqrt{17}< 9< 16$
7 tháng 8 2021
Áp dụng bđt bunhia copski ta có:
`(sqrt2+sqrt3)^2<=(1+1)(2+3)`
`<=>(sqrt2+sqrt3)^2<=2.5=10`
`=>sqrt2+sqrt3<=sqrt{10}`
Dấu "=" không xảy ra
`=>sqrt2+sqrt3<sqrt{10}`
7 tháng 8 2021
Ta có \(\left(\sqrt{2}+\sqrt{3}\right)^2=5+2\sqrt{6};\left(\sqrt{10}\right)^2=10=5+5\)
Mà \(\left(2\sqrt{6}\right)^2=24;5^2=25\)
\(\Rightarrow2\sqrt{6}< 5\Rightarrow\left(\sqrt{2}+\sqrt{3}\right)^2< \left(\sqrt{10}\right)^2\)
\(\Rightarrow\sqrt{2}+\sqrt{3}< \sqrt{10}\)
7 tháng 8 2021
Ta có \(\left(\sqrt{2018}+\sqrt{2020}\right)^2=4038+2\sqrt{4076360}\) và \(\left(2\sqrt{2019}\right)^2=8076=4038+4038\)
Mà \(\left(2\sqrt{4076360}\right)^2=16305440\) và \(4038^2=16305444\)
\(\Rightarrow2\sqrt{4076360}< 4038\)
\(\Rightarrow\sqrt{2018}+\sqrt{2020}< 2\sqrt{2019}\)
7 tháng 8 2021
\(\left(\sqrt{2018}+\sqrt{2020}\right)^2=4038+2\cdot\sqrt{2018\cdot2020}\)
\(\left(2\sqrt{2019}\right)^2=8076=4038+4038\)
mà \(2\cdot\sqrt{2018\cdot2020}< 4038\)
nên \(\sqrt{2018}+\sqrt{2020}< 2\sqrt{2019}\)
TD
2
7 tháng 9 2023
Máy tính điện tử ENIAC | Máy tính bảng mỏng nhẹ hiện nay |
Kích thước rất lớn | Kích thước nhỏ, gọn, dễ dàng mang theo người. |
Tiêu thụ nhiều điện | Tiêu thụ ít điện |
Khi hoạt động tỏa ra nhiều nhiệt lượng và không đảm bảo kết quả luôn đáng tin cậy. | Khi hoạt động tỏa ra ít nhiệt lượng và đảm bảo kết quả luôn đáng tin cậy. |
Chưa có nhiều tính năng khác. | Có nhiều tính năng khác. |
⇒ Sự phát triển của máy tính diễn ra nhanh chóng và đạt được nhiều thành tựu to lớn.
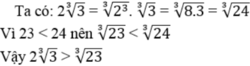
ai bt đc
ko bt đừng làm / đăng