△ABC (AB < AC), AD là tia phân giác. Trên tia đối của DA lấy I sao cho ACI = BDA. Cma. Δ ADBđồng dạng ΔACI

2N

28 Nhật Quý

10 tháng 3 2022 - olm

△ABC (AB < AC), AD là tia phân giác. Trên tia đối của DA lấy I sao cho ACI = BDA. Cma. Δ ADBđồng dạng ΔACI;Δ ADB đòng dạng ΔACDI(ko cần làm) | bổ sung: AD2 = AB. AC - DB. DCb. Gọi M là trung điểm BC, các tia phân giác của AMB và AMC cắt AB, AC theo thứ tự tại E, F. Cm EF//BC(ko cần làm)c. Gọi H là giao điểm của EF và AM. Cm AH.BE =...

Đọc tiếp

#Toán lớp 8

0

2N

28 Nhật Quý

10 tháng 3 2022

△ABC (AB < AC), AD là tia phân giác. Trên tia đối của DA lấy I sao cho ACI = BDA. Cma. Δ ADBđồng dạng ΔACI;Δ ADB đòng dạng ΔACDI(ko cần làm) | bổ sung: AD2 = AB. AC - DB. DCb. Gọi M là trung điểm BC, các tia phân giác của AMB và AMC cắt AB, AC theo thứ tự tại E, F. Cm EF//BC(ko cần làm)c. Gọi H là giao điểm của EF và AM. Cm AH.BE =...

Đọc tiếp

#Toán lớp 8

0

PT

Pham Trong Bach

8 tháng 4 2019

Cho tam giác ABC (AB < AC), đường phân giác trong AD. Trên tia đối của tia DA lấy điểm I sao cho A C I ^ = B D A ^ . Chứng minh:a) Δ A B D ∽ Δ A I C ; b) Δ A B D ∽ Δ C I D ; c) A D 2 = A B . A C − D B . D C . ...

Đọc tiếp

#Toán lớp 8

1

CM

Cao Minh Tâm

8 tháng 4 2019

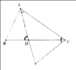
a) HS tự chứng minh.

b) HS tự chứng minh.

c) Từ a, suy ra AB.AC = AD.AI (1)

Từ b, suy ra BD.CD = AD.ID (2)

Từ (1) và (2), ta chứng minh được AD² = AB.AC- DB.DC

Đúng(0)

QL

Quang le

25 tháng 3 2017 - olm

cho tam giác ABC vuông tại A có AB =3cm AC=4cm AD là tia phân giác của góc BAC (D thuộc BC)

a) tính BD

b)trên tia đối của tia DA lấy điểm I sao cho góc ACI= góc BDA chứng minh tam giác ABD đồng dạng tam giác ACI

#Toán lớp 8

0

NV

Nguyễn Vi Thảo

28 tháng 4 2016 - olm

Cho tam giác ABC (AB<AC) đừơng phân giác AD (D thuộc BC). Trên tia đối cuả DA lấy điểm I sao cho góc ACI = góc BDA. Chứng minh rằng. a) -Tam giác ADB đồng dạng tam giác ACI -Tam giác ADB đồng dạng tam giác CDI

b) AD bình phương=AB.AC-DB.DC

#Toán lớp 8

0

TP

Trương Phương Anh

17 tháng 4 2016 - olm

Cho tam giác ABC có AB=6, AC=10, BC=12. Vẽ đường phân giác AD của góc BAC, trên tia đối tia DA lấy điểm I sao cho góc ACI=góc BDA.

a) Tính DB và DC

b) Chứng minh ∆ACI đồng dạng ∆CDI

c)Chứng minh AD^2=AB.AC - DB.DC

#Toán lớp 8

0

MS

Minamoto Sizuka

1 tháng 5 2021 - olm

cho tam giác ABC có AB= 6cm, AC=10 cm và BC=12cm. vẽ đường phân giác AD của góc BAC, trên của tia DA lấy điểm I sao cho góc ACI=góc BDA

c/m tam giác ACI đồng dạng với Tam giác CDI

#Toán lớp 8

0

TL

Thi Luyen Dao

11 tháng 5 2020 - olm

Cho tam giác ABC (AB<AC), AD là đường phân giác của góc A(D thuộc BC). Trên tia đối của tia DA lấy điểm I sao cho góc ACI = góc ABD. Chứng minh a, tam giác ABD đồng dạng tam giác ACI b, tam giác CDI cân c,AD.CD=AI.BD

#Toán lớp 8

9

LM

Lê Mai Giang

11 tháng 5 2020

Câu hỏi kiểu j vậy bn ????

Đúng(0)

BT

Bùi thiện huy thịnh

11 tháng 5 2020

Bạn ơi gửi câu hỏi cho đàng hoàng đấy

Đúng(0)

AH

ahn heeyeon

19 tháng 3 2019

cho tam giác ABC có AB=6cm,AC=10cm,BC=12cm.vẽ đường phân giác AD

a/tính BD

b/trên tia đối của tia DA lấy điểm I sao cho góc ACI=ADB.C/mΔADBđồng dạng ΔACI

c/C/m AD^2=AB.AC-BD.CD

#Toán lớp 8

1

NT

ngo trong tuan

19 tháng 3 2019

TỚ TRÌNH BÀY KO ĐẸP MONG CẬU thông cảm

a) có AD là tia p/g của góc ABC => \(\frac{BD}{DC}\)=\(\frac{AB}{AC}\)=> \(\frac{BD}{DC}\)=\(\frac{3}{5}\)<=>\(\frac{BD}{3}\)=\(\frac{DC}{5}\). Ap dụng t/c của dãy tỉ số bằng nhau ta có :\(\frac{BD}{3}\)=\(\frac{DC}{5}\)<=>\(\frac{BD+DC}{3+5}\)=\(\frac{12}{8}\)=\(\frac{3}{2}\)=> BD =4,5

B) △ADB ∼△ACI (g.g) do có góc ADB =^ACI (gt) và có ^A1=^A2( 2 góc tia p/g ,bạn có thể đọc hẳn tên góc)

c) có 2 △trên đồng dạng ( chứng minh câu b) =>\(\frac{AD}{AC}\)=\(\frac{AB}{AI}\)=> AD. AI =AB. AC(1)

XÉT △DBA và △DIC , CÓ : ^BDA =^IDC ( 2 góc đối đỉnh) và ^DBC=^DIC( do △ADB ∼△ACI) => △DBA ∼△DIC (g.g) => \(\frac{AD}{CD}\)=\(\frac{BD}{DI}\)=> AD.DI =BD.CD(2). Ta lấy biểu thức (1) - b/t (2) sẽ ra điều phải c/m như sau :( CHÚ Ý VT1 -VT2 VP cũng như vậy)

AD.AI - AD.DI =AB.DC -BD .CD <=> AD( AI-DI) =AB.DC-BD.CD<=>\(AD^2\)=AB.DC- BD.CD

Đúng(0)

HN

Hieu Ngoc Nguyen

14 tháng 7 2021

Bài 1 : Cho tam giác ABC có AB=6cm ; AC=10cm ; BC=12cm . Vẽ đường phân giác AD của góc A . Trên tia đối của tia DA lấy điểm I sao cho góc ACI = góc BDA

a) Tính DB , DC

b) Chứng minh tam giác ACI đồng dạng với tam giác CDI

c) Chứng minh AD^2=AB.AC-DB.DC

#Toán lớp 8

1

HT

Huỳnh Thị Thanh Ngân

17 tháng 7 2021

a) DB?, DC?

Ta có:\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(tính chất đường phân giác)

⇒\(\dfrac{DB}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)

Mặt khác \(\dfrac{DB}{3}=\dfrac{DC}{5}\)

\(\dfrac{DB}{3}=\dfrac{DC}{5}=\dfrac{DB+DC}{3+5}=\dfrac{BC}{8}=\dfrac{12}{8}=\dfrac{3}{2}\)

\(\dfrac{DB}{3}=\dfrac{3}{2}\\ \Rightarrow DB=\dfrac{3\times3}{2}=\dfrac{9}{2}=4.5\left(cm\right)\)

Và \(\dfrac{DC}{5}=\dfrac{3}{2}\\ \Rightarrow DC=\dfrac{3\times5}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)

Vậy DB=4,5(cm), DC= 7,5 cm

Đúng(2)

TL

Thi Luyen Dao

11 tháng 5 2020 - olm

Cho tam giác ABC(AB<AC), AD là đường phân giác của góc A(D thuộc BC). Trên tia đối của tia DA lấy điểm I sao cho góc ACI= góc ABD. Chứng minh

a, tam giác ABD đồng dạng tam giác ACI

b, tam giác CDI cân

c, AD.CD=AI.BD

#Toán lớp 8

2

KL

Khánh Linh

11 tháng 5 2020

Bạn ơi hình như thiếu đề

Đúng(0)

T

thắng

11 tháng 5 2020

nếu câu hỏi là như này

Cho Tam Giác ABC ( AB<AC) , đường phân giác DA .Trên tia đối của tia DA lấy điểm I sao cho góc ACI = góc BAD . Chứng minh:

a. tam giac ADB và tam giác ACI đồng dạng

b. tam giác ADB và tam giác CDI đồng dạng

c. AD^2 = AB.AC - DB.BC

mk trả lời này

a.Xét tgiac ADB và tgiac ACI có:

góc BAD = góc IAC(gt)

góc BDA= góc ICA(gt)

Vậy tgiac ADB đồng dạng với tgiac ACI(g.g)

=> góc ABD = góc AIC => góc ABD = góc DIC

b.xét tgiac ADB và tgiac CDI có:

góc ADB= góc CDI(đối đỉnh)

góc ABD= góc CID(cmt)

vậy tgiac ADB đồng dạng với tgiac CDI(g.g)

c.theo câu a tgiac ADB đồng dạng với tgiac ACI nên ta có:

AD/AC=AB/AI=> AB.AC=AD.AI(1)

theo câu b ta lại có tgiac ADB đồng dạng với tgiac CDI nên ta có:

BD/DI=AD/CD=> BD.CD=DI.AD(2)

TỪ (1) VÀ (2) ta có:

AB.AC-DB.DC=AD.AI-DI.AD=AD.(AI-DI)=AD.AD=AD²(ĐPCM)

nếu đúng đề bài thì k mk nha

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP