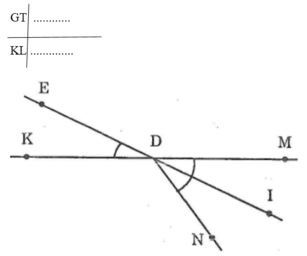
Gọi ID là tia phân giác của góc MDN. Gọi góc EDK là góc đối đỉnh của IDM. Chứng minh rằng: EDK = ID
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chứng minh:
∠(IDM) =∠(IDN) (vì DI là tia phân giác của ∠(MDN) (1)
∠(IDM) =∠(EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠(EDK) =∠(IDN) (điều phải chứng minh)

GT: DI là tia phân giác của \(\widehat{MDN}\)
\(\widehat{EDK}\) đối đỉnh với \(\widehat{IDM}\)
KL: \(\widehat{EDK}=\widehat{IDM}\)
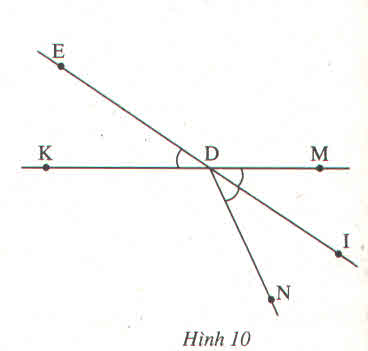
Chứng minh (h.10)
ˆIDM=ˆIDNIDM^=IDN^ (vì DI là tia phân giác của \(\widehat{MDN}\)) (1)
ˆIDM=ˆEDKIDM^=EDK^ (vì 2 góc này đối đỉnh) (2)
Từ (1) và (2) suy ra \(\widehat{EDK}=\widehat{IDN}\)

GT KL DI là tia phân giác của MDN EDK đối đỉnh với IDM EDK = IDN
Chứng minh:
\(\widehat{IDM}=\widehat{IDN}\) ( vì \(DI\) là tia pân giác của \(\widehat{MDN}\)) (1)
\(\widehat{IDM}=\widehat{EDK}\) ( hai góc đối đỉnh )
Từ (1) và (2) suy ra : \(\widehat{EDK}=\widehat{IDN}\left(đpcm\right)\)
Chúc bạn học tốt!
Ta có: Chứng minh:IDM=IDN (Vì DI là tia phân giác của MDN ) (1)
Ta có: IDM=EDK (Vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra: EDK=IDN (điều phải chứng minh)

1) đề thiếu nhé
2) Sửa lại : AM | BC
+) Góc A + B + C = 180o => A + 50o + 50o = 180o => A = 80o
=> góc BAM = A/2 = 40o
+) Tam giác BAM có: góc BAM + B + AMB = 180o => 40o + 50o + AMB = 180o => AMB = 90o
=> AM | BC

vì hai góc AOB và COD là hai đối đỉnh mà hai góc đối đỉnh thì bằng nhau và 2goc đó mỗi góc được một tia phân giác phân thành hai góc bằng nhau và tạo thành một tia đối .