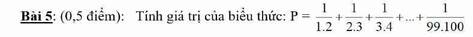giúp mik vs nha mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QN
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
1
29 tháng 7 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: AH=căn 5^2-3^2=4cm
BI là phân giác
=>HI/HB=IA/AB
=>HI/3=IA/5=(HI+IA)/(3+5)=0,5
=>HI=1,5cm; IA=1,5cm
mn giúp mik vs nha
HN
1 tháng 8 2021
1, I'm so ............excited..... about your trip . It's going to be amazing ( excite )
2, Ao Dai is us=> our ..........traditional......... dress . We wear it every Monday at school ( tradition )
3, In Vietnam , we usually wait for the ...............elderly..... person to sit down before you sit down ( old )
4, After .............taking..... food from the plate you should put it into your bowl before eating ( take )
5, What is the ..........similarity.......between a custom and a tradition ( similer)
giúp mik vs nha mn
12 tháng 1 2022
c: \(=\left(157-81\right):4-3^3=19-27=-8\)
d: \(=250:\left\{5\cdot\left[88\cdot1-2024+1946\right]\right\}=250:50=5\)
22 tháng 11 2021
\(n_{CuSO_4}=0,2x\left(mol\right)\)
\(Fe+CuSO_4\rightarrow FeSO_4+Cu\)
0,2x 0,2x 0,2x
\(m_{tăng}=m_{Cu}-m_{Fe}=64\cdot0,2x-56\cdot0,2x=1,6\)
\(\Rightarrow x=1M\)
Chọn C.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
22 tháng 11 2021
\(n_{Fe}=n_{FeSO_4}=n_{Cu}=n_{CuSO_4}=0,2.x\left(mol\right)\\ Fe+CuSO_4\rightarrow FeSO_4+Cu\\ m_{t\text{ăn}g}=m_{Cu.b\text{á}m.v\text{ào}}-m_{Fe.tan.ra}\\ \Leftrightarrow1,6=64.0,2x-56.0,2x\\ \Leftrightarrow x=1\\ \Rightarrow C\)
mn giúp mik vs mik cần gấp( có trình bày nha~)
15 tháng 12 2021
Gọi thời gian của T,D,M lần lượt là \(a,b,c(giờ;a,b,c>0)\)
Áp dụng tc dtsbn:
\(10a=9b=8c\Leftrightarrow\dfrac{10a}{360}=\dfrac{9b}{360}=\dfrac{8c}{360}\Leftrightarrow\dfrac{a}{36}=\dfrac{b}{40}=\dfrac{c}{45}=\dfrac{c-a}{45-36}=\dfrac{0,3}{9}=\dfrac{1}{30}\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{6}{5}\\b=\dfrac{4}{3}\\c=\dfrac{3}{2}\end{matrix}\right.\)
Vậy ...
3 tháng 7 2023
5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C
4 tháng 11 2023
1:
\(A=\dfrac{2}{3}+\dfrac{8}{9}+...+\dfrac{3^n-1}{3^n}\)
\(=1-\dfrac{1}{3}+1-\dfrac{1}{3^2}+...+1-\dfrac{1}{3^n}\)
\(=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
Đặt \(B=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\)
=>\(3B=1+\dfrac{1}{3^1}+...+\dfrac{1}{3^{n-1}}\)
=>\(2B=1+\dfrac{1}{3}+...+\dfrac{1}{3^{n-1}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^n}=1-\dfrac{1}{3^n}\)
=>\(2B=\dfrac{3^n-1}{3^n}\)
=>\(B=\dfrac{1}{2}-\dfrac{1}{2\cdot3^n}< \dfrac{1}{2}\)
\(A=n-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^n}\right)\)
\(=n-B>n-\dfrac{1}{2}\)
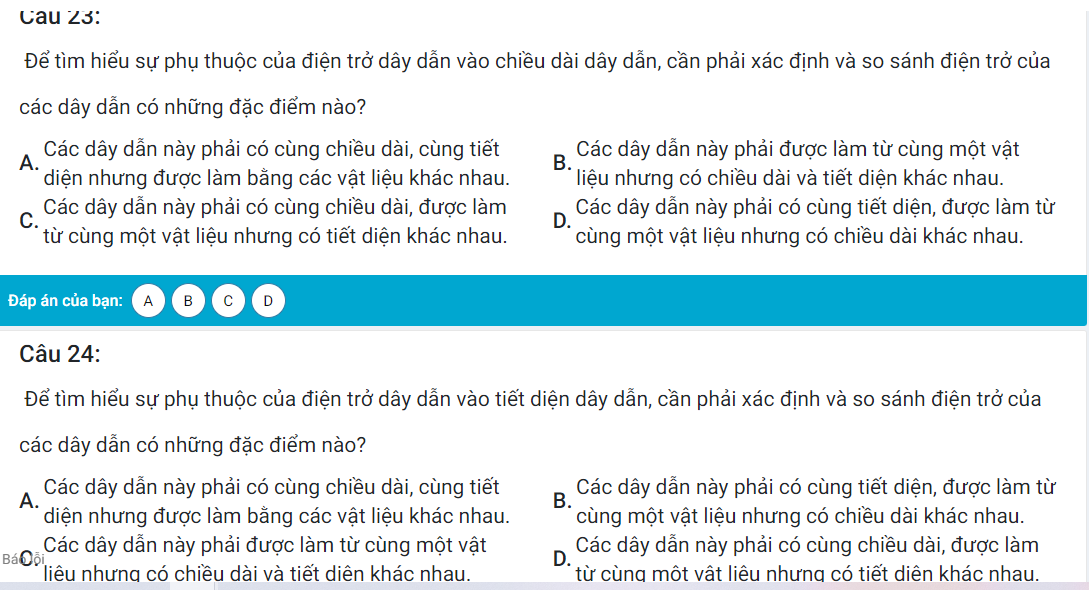
\(P=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
\(=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
P=1-1/2+1/2-1/3+1/3-1/4+...+1/99-1/100
=1+(1/2-1/2)+(1/3-1/3)+...+(1/99-1/99)-1/100
=1+0+0+0+...+0-1/100
=1-100
=100/100-1/100
=99/100