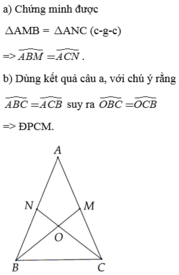
Cho tam giác ABC cân tại A. Trên cạnh AB và Ac lần lượt lấy 2 điểm M và N sao cho AM =AN , chứng minh tứ giác MNCB là hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
a: Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Do đó: MN//BC
Xét tứ giác MNCB có MN//BC
nên MNCB là hình thang
mà \(\widehat{C}=\widehat{B}\)
nên MNCB là hình thang cân
11 tháng 7 2023
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét tứ giác MNCB có
MN//BC
góc B=góc C
=>MNCB là hình thang cân
KK
3 tháng 12 2018
Cho tam giác ABC cân tại A. Trên đường thẳng đi qua đỉnh A song song với BC lấy hai điểm M và N sao cho A là trung điểm của MN (M và B cùng thuộc nửa mặt phẳng bờ là AC). Gọi H, I, K lần lượt là trung điểm MB, BC, CN. a) Chứng minh tứ giác MNCB là hình thang cân. b) Tứ giác AHIK là hình gì? Vì sao - Toán học Lớp 8 - Bài tập Toán học Lớp 8 - Giải bài tập Toán học Lớp 8 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
3 tháng 8 2021
a) Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC và \(MN=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay \(BC=2\cdot MN=2\cdot8=16\left(cm\right)\)
b) Xét tứ giác BMNC có MN//BC(cmt)
nên BMNC là hình thang(Định nghĩa hình thang)
Hình thang BMNC có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BMNC là hình thang cân
23 tháng 9 2021
Xét ΔABC có
\(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
Do đó: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
TH
25 tháng 12 2021
Bạn Minh Anh bạn đã tìm được đáp án ch vậy , cho tôi xin đáp án với vì câu hỏi của tôi y hệt bạn mà hỏi kh ai trl