Cho tam giác CUP vuông tại C, CK là đường cao kẻ từ C Tìm một phép đồng dạng biến tam giác KUP thành tam giác CUP
o O O nguyễn tuán anh ê ,giải mk bài này mk tích cho bshn 1 tuần liền ok
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cho hỏi làm như này đúng ko:
Gọi e là đường phân giác củaU . Ta có Ee biến ∆CUG thành ∆C'U'P'. biến ∆C'U'P' thành ∆CUP
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp Ee và sẽ tam giác CUG thành tam giác CUP
là xog r đấy ,
nguyễn tuấn anh;có thiếu dữ klieeju ko ,các pạn cho mk hỏi ,làm như z đúng chưa ạ

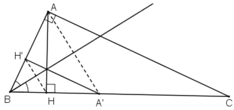
Gọi d là đường phân giác của góc B của ΔABC.
+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B
(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).
⇒ ΔH’BA’ = Đd(ΔHBA).
⇒ ΔH’BA’ = ΔHBA.
Mà ΔABC 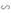 ΔHBA theo tỉ số
ΔHBA theo tỉ số 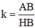
⇒ ΔABC  ΔH’BA’ theo tỉ số k
ΔH’BA’ theo tỉ số k
⇒ AB = k.H’B; BC = k.BA’.
Mà A ∈ tia BH’ ; C ∈ tia BA’
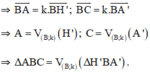
Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số 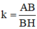 hợp với phép đối xứng trục d là phân giác của
hợp với phép đối xứng trục d là phân giác của 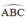

Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.
Gọi d là đường phân giác của . Ta có
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và Dd sẽ biến
HBA thành
ABC.

a: Xét ΔMIN vuông tại I có IE là đường cao ứng với cạnh huyền MN
nên \(ME\cdot MN=MI^2\left(1\right)\)
Xét ΔMIP vuông tại I có IF là đường cao ứng với cạnh huyền MP
nên \(MF\cdot MP=MI^2\left(2\right)\)
Từ (1) và (2) suy ra \(ME\cdot MN=MF\cdot MP\)
hay \(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Xét ΔMEF vuông tại M và ΔMPN vuông tại M có
\(\dfrac{ME}{MP}=\dfrac{MF}{MN}\)
Do đó: ΔMEF\(\sim\)ΔMPN

a: Xét ΔACI vuông tại C và ΔAHB vuông tại H có
góc CAI=góc HAB
=>ΔACI đồng dạng với ΔAHB
b: Xét ΔHBI và ΔHAB có
góc HBI=góc HAB
góc H chung
=>ΔHBI đồng dạng với ΔHAB
=>HB/HA=HI/HB
=>HB^2=HA*HI
c: CD/DA=CK/KA=CB/CA
a.
Xét hai tam giác AIC và ABH có:
\(\left\{{}\begin{matrix}\widehat{CAI}=\widehat{BAH}\left(\text{Ax là phân giác}\right)\\\widehat{ACI}=\widehat{AHB}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIC\sim\Delta ABH\left(g.g\right)\) (1)
b.
Xét hai tam giác AIC và BIH có:
\(\left\{{}\begin{matrix}\widehat{AIC}=\widehat{BIH}\left(\text{đối đỉnh}\right)\\\widehat{ACI}=\widehat{BHI}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AIC\sim\Delta BIH\left(g.g\right)\) (2)
(1);(2) \(\Rightarrow\Delta ABH\sim\Delta BIH\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{BH}{IH}\Rightarrow BH^2=HI.HA\)
c.
Áp dụng định lý phân giác trong tam giác ACK: \(\dfrac{CD}{DA}=\dfrac{CK}{AK}\) (3)
Xét hai tam giác ABC và ACK có:
\(\left\{{}\begin{matrix}\widehat{CAB}\text{ chung}\\\widehat{BCA}=\widehat{CKA}=90^0\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{BC}{CK}=\dfrac{AC}{AK}\Rightarrow\dfrac{BC}{AC}=\dfrac{CK}{AK}\) (4)
(3);(4) \(\Rightarrow\dfrac{CD}{DA}=\dfrac{BC}{AC}\)
Mik quên còn t/c đường phân giác nữa
Sorry nha
Nhưng chưa chắc đúng đâu sơ xài quá
Bài này ẩu kinh
Bạn biết phép đông dạng gồm :
Góc - Góc
Cạnh Cạnh cạnh
Cạnh canh góc
Ở đây thứ nhất thiếu dữ liệu
Thứ 2 thiếu hình
Thứ 3 chơi xỏ mik