Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

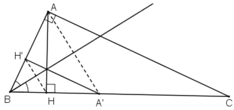
Gọi d là đường phân giác của góc B của ΔABC.
+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B
(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).
⇒ ΔH’BA’ = Đd(ΔHBA).
⇒ ΔH’BA’ = ΔHBA.
Mà ΔABC 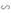 ΔHBA theo tỉ số
ΔHBA theo tỉ số 
⇒ ΔABC  ΔH’BA’ theo tỉ số k
ΔH’BA’ theo tỉ số k
⇒ AB = k.H’B; BC = k.BA’.
Mà A ∈ tia BH’ ; C ∈ tia BA’
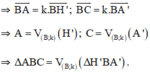
Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số 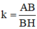 hợp với phép đối xứng trục d là phân giác của
hợp với phép đối xứng trục d là phân giác của 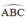


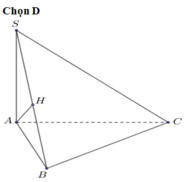
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.

a) xét tam giác ADB và AEC có:
góc A chung
góc ADB= góc AEC (=90 độ)
=> ADB đồng dạng vs AEC (g.g)
b) xét tam giác EHB và tam giác DHC có:
EHB= DHC (2 góc đối đỉnh)
HEB- HDC (=90độ)
=> EHB =DHC (g.g)
=> HE/HB = HD/HC
=> HE.HC=HD.HB

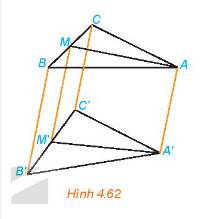
MN là đường trung bình của tam giác ABC
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.

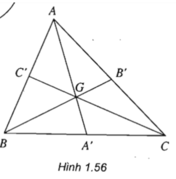
Theo đề bài ta có: AA', BB', CC' là các đường trung tuyến của ΔABC ⇒ G là trọng tâm
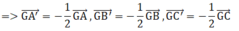
Vậy phép vị tự tâm G, tỉ số k = -1/2 biến tam giác ABC thành tam giác A'B'C'



Gọi d là đường phân giác của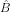 . Ta có
. Ta có 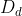 biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp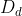 và Dd sẽ biến
và Dd sẽ biến 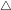 HBA thành
HBA thành 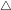 ABC.
ABC.
Gọi d là đường phân giác của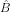 . Ta có
. Ta có 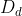 biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
biến ∆HBA thành ∆A'B'C'. Dd biến ∆A'B'C' thành ∆ABC.
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp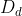 và Dd sẽ biến
và Dd sẽ biến 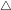 HBA thành
HBA thành  ABC.
ABC.