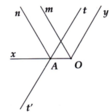
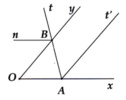
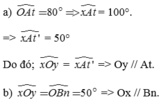Cho góc xÔy =60° và điểm A thuộc tia Ox(A ≠ O)Trên nửa mặt phẳng bờ chứa tia Ox không chứa tia oy.Vẽ tia At sao cho góc xAt=120°. Chứng tỏ rằng đường thẳng chứa tia Oy và At song song với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PA
12 tháng 7 2016
Bạn tự vẽ hình nha
a.
OAt + tAx = 1800 (2 góc kề bù)
1000 + tAx = 1800
tAx = 1800 - 1000
tAx = 800
Am là tia phân giác của tAx
=> tAm = mAx = \(\frac{tAx}{2}=\frac{80^0}{2}=40^0\)
mà xOy = 400
=> xOy = xAm
mà 2 góc này ở vị trí đồng vị
=> Oy // Am
b.
Bn // Ox
<=> nBO = xOB (2 góc so le trong)
mà xOB = 400
=> nBO = 400
Chúc bạn học tốt
PA
11 tháng 7 2016
Bạn tự vẽ hình nha
a.
OAt + tAx = 1800 (2 góc kề bù)
1000 + tAx = 1800
tAx = 1800 - 1000
tAx = 800
Am là tia phân giác của tAx
=> tAm = mAx = \(\frac{tAx}{2}=\frac{80^0}{2}\) = 400
mà xOy = 400
=> xOy = xAm
mà 2 góc này ở vị trí đồng vị
=> Am // Oy
b.
Bn // Ox
<=> nBO = xOB (2 góc so le trong)
mà xOB = 400
=> nBO = 400
Chúc bạn học tốt
M
16 tháng 9 2020
Bài giải
a.
\(\widehat{OAt }+\widehat{ tAx }=180^o\) (2 góc kề bù)
\(100^o+\widehat{tAx}=180^o\)
\(\widehat{tAx}=80^o\)
Am là tia phân giác của \(\widehat{tAx}\)
=> \(\widehat{tAm}\) = \(\widehat{mAx}\) = \(\frac{\widehat{tAx}}{2}=\frac{80^o}{2}=40^o\)
mà \(\widehat{xOy}=40^o\)
=> \(\widehat{xOy}=\widehat{xAm}\)
mà 2 góc này ở vị trí đồng vị
=> Oy // Am
b.
Bn // Ox
<=> \(\widehat{nBO}=\widehat{xOB}\) (2 góc so le trong)
mà \(\widehat{xOB}=40^o\)
=>\(\widehat{nBO}=40^o\)
CM
30 tháng 12 2018
a) O A t ^ + x O y ^ = 60°+ 120° = 180° (hai góc trong cùng phía bù nhau)
=> At // Oy => tt' // Oy
b) Vì Om là phân giác x O y ^ nên:
x O m ^ = 1 2 x O y ^ = 1 2 .120° = 60° (1)
Mặt khác : O A t ^ = 60 ° = > x A t ^ = 120°
Vì An là phân giác x A t ^ nên:
x A n ^ = 1 2 x A t ^ = 1 2 .120° = 60° (2)
Từ (1) và (2) suy ra x O m ^ = x A n ^ .
Do đó Om // An
