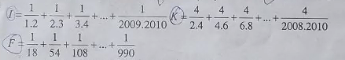
Giải chi tiết giúp mik nha.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
Giải chi tiết giúp mik nha
6
VD
22 tháng 3 2022
\(a,2+\dfrac{2}{3}=\dfrac{6}{3}+\dfrac{2}{3}=\dfrac{8}{3}\\ \dfrac{6}{9}-\dfrac{6}{11}=\dfrac{66}{99}-\dfrac{54}{99}=\dfrac{12}{99}=\dfrac{4}{33}\\ b,21\times\dfrac{4}{7}=12\\ \dfrac{54}{30}:\dfrac{6}{5}=\dfrac{9}{5}\times\dfrac{5}{6}=\dfrac{3}{2}\)
KN
Giải chi tiết giúp mik nha!!
2
O
30 tháng 3 2022
\(y:\dfrac{3}{11}=\dfrac{7}{6}+\dfrac{2}{3}\)
\(y:\dfrac{3}{11}=\dfrac{11}{6}\)
\(y=\dfrac{11}{6}\times\dfrac{3}{11}\)
\(y=\dfrac{1}{2}\)
Bài 3
\(\dfrac{3}{7}:\dfrac{1}{4}-\dfrac{1}{2}=\dfrac{3}{7}\times\dfrac{4}{1}-\dfrac{1}{2}=\dfrac{12}{7}-\dfrac{1}{2}=\dfrac{24}{14}-\dfrac{7}{14}=\dfrac{17}{14}\)
NA
30 tháng 3 2022
`2)`
`y:3/11=7/6+2/3`
`y:3/11=11/6`
`y=11/6xx3/11`
`y=1/2`
`3)`
`=12/7-1/2=24/14-7/14=17/14`
14 tháng 3 2022
`7/12 + 3/4 xx 2/9`
`= 7/12 + 1/6`
`= 9/12`
_________________
`8/9 - 4/15 : 2/5`
`= 8/9 - 2/3`
`= 2/9`
DT
1
HQ
Hà Quang Minh
Giáo viên
31 tháng 7 2023
\(A=\dfrac{31\cdot\left(31^{12}-1\right)}{31\left(31^{13}+1\right)}=\dfrac{31^{13}+1-32}{31\left(31^{13}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{14}+31}\)
\(B=\dfrac{31\left(31^{13}-1\right)}{31\left(31^{14}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Dễ thấy \(31^{14}+31< 31^{15}+31\Rightarrow\dfrac{32}{31^{14}+31}>\dfrac{32}{31^{15}+31}\\ \Rightarrow\dfrac{1}{31}-\dfrac{32}{31^{14}+31}< \dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Vậy A < B
C0
2
3 tháng 10 2021
c) \(=\left(4x-3\right)^2-\left(9x^2-4\right)\)
\(=16x^2-24x+9-9x^2+4=7x^2-24x+13\)
d) \(=\left(x^2-3x+2\right)\left(x+3\right)-\left(x^3-5x^2\right)\)
\(=x^3+3x^2-3x^2-9x+2x+6-x^3+5x^2\)
\(=5x^2-7x+6\)
HP
3 tháng 10 2021
c. (4x - 3)(4x - 3) - (3x + 2)(3x - 2)
= (4x - 3)2 - (9x2 - 4)
= 16x2 - 24x + 9 - 9x2 + 4
= 16x2 - 9x2 - 24x + 9 + 4
= 7x2 - 24x + 13
d. (x - 2)(x - 1)(x + 3) - x2(x - 5)
= (x2 - 1 - 2x + 2)(x + 3) - x2(x - 5)
= x3 + 3x2 - x - 3 - 2x2 - 6x + 2x + 6 - x3 + 5
= x3 - x3 + 3x2 - 2x2 - x - 6x + 2x + 6 + 5 - 3
= x2 - 5x + 8
giải nhanh và chi tiết giúp mik nha!
L
14 tháng 5 2022
= 26 x 182 + 182 x 47 + 91 x 27 x 2
= 26 x 182 + 182 x 47 + 182 x 27
= 182 x ( 26 + 47 + 27)
= 182 x 100 = 18200
NV
2
\(I=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2009.2010}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2010}\\ =1-\dfrac{1}{2010}\\ =\dfrac{2009}{2010}\)
\(K=\dfrac{4}{2.4}+\dfrac{4}{4.6}+...+\dfrac{4}{2008.2010}\\ =2\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{2008.2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}\right)\\ =2\left(\dfrac{1}{2}-\dfrac{1}{2010}\right)\\ =2.\dfrac{502}{1005}\\ =\dfrac{1004}{1005}\)
\(F=\dfrac{1}{18}+\dfrac{1}{54}+...+\dfrac{1}{990}\\ =\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{30.33}\\ =\dfrac{1}{3}\left(\dfrac{3}{3.6}+\dfrac{3}{6.9}+...+\dfrac{3}{30.33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}.\dfrac{10}{33}\\ =\dfrac{10}{99}\)
\(I=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2009}-\dfrac{1}{2010}=\dfrac{2010-1}{2010}=\dfrac{2008}{2010}\)
\(K=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{2008}-\dfrac{1}{2010}=\dfrac{502}{1005}\)
\(F=\dfrac{1}{3.6}+\dfrac{1}{6.9}+...+\dfrac{1}{99.100}=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{100}\right)=\dfrac{97}{900}\)