Bài 13: Cho tam giác ABC có AM là phân giác và AB > AC. Lấy I thuộc AB sao cho AI = AC
a) So sánh MC với MI.
b) Chứng minh: MB - MC < AB- AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2020
Câu 1)
A )Ta có tam giác ABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\)
Và AB = AC
Xét hai tam giác vuông BCK và CBH ta có :
BC chung
\(\widehat{KBC}=\widehat{BCH}\)
=>BCK = CBH (cạnh huyền - góc nhọn )
=>BH = CK (đpcm)
B) ta có BCK = CBH
=> \(\widehat{HBC}=\widehat{KCB}\)
=> \(\widehat{ABH}=\widehat{ACK}\)
=> tam giác OBC cân tại O
=> BO = CO
Xét tam giác ABO và tam giác ACO
AB = AC
BO = CO (cmt)
\(\widehat{ABH}=\widehat{ACK}\)
=> ABO=ACO (c-g-c)
=> \(\widehat{BAO}=\widehat{CAO}\)
=> AO là phân giác góc ABC (đpcm)
C) ta có
AI là phân giác góc ABC
Mà tam giác ABC cân tại A
=> AI vuông góc với cạnh BC (đpcm)
9 tháng 5 2018
a) Bạn xét 2 tam giác ABM và tam giác ADM ( c-g-c )
Suy ra BM = DM ( 2 cạnh tương ứng )
b) Xét 2 tam giác AKD và tam giác ACB ( g-c-g )
Suy ra AK = AC ( 2 cạnh tương ứng )
Suy ra tan giác AKC cân tại A
Mấy cái tam giác bằng nhau bạn tự chứng minh
PL
19 tháng 2 2021
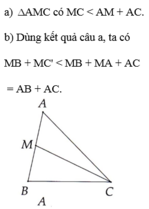
a) trong một tam giác thì tổng độ dài 2 cạnh bát kì luôn lớn hơn cạnh còn lại nên
tam giác AMC có AM + AC > CM
b) vì M thuộc cạnh AB nên AM + MB = AB
ta có: \(AB+AC=AM+MB+AC=\left(AM+AC\right)+MB\)
mà \(AM+AC>MC\)(cmt) \(\Rightarrow AB+AC=\left(AM+AC\right)+MB>MC+MB\)
vậy \(AB+AC>MC+MB\)
19 tháng 2 2021
BVì M thuộc trong tam giác ABC nên tia BM thuộc trong B , nó cắt AC Tại D
D nằm giữa A và C, M nằm giữa B và D
Trong Tam giác BAD có
BM + MD < BA + AD + DCTRong tam giác MDC có MC - MD < DC
Cộng 2 vế của 1 và 2 với nhau ta được : BM +MC
CÒn phần sau mình chưa làm xin lỗi bạn
12 tháng 5 2023
Xét ΔBAM và ΔCAM có
AM chung
góc BAM=góc CAM
AB=AC
=>ΔBAM=ΔCAM
=>MB=MC và góc AMB=góc AMC=180/2=90 độ
=>AM vuông góc BC