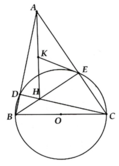
Cho tam giác $ABC$ có ba góc nhọn. Đường tròn $(O)$ đường kính $BC$ cắt các cạnh $AB$, $AC$ tại các điểm $D$ và $E$. Gọi $H$ là giao điểm của hai đường thẳng $BE$ và $CD$.
a) Chứng minh tứ giác $ADHE$ nội tiếp trong một đường tròn. Xác định tâm $I$ của đường tròn này.
b) Gọi $M$ là giao điểm của $AH$ và $BC$. Chứng minh $CM.CB = CE.CA$.