Cíu mình bài chia động từ này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mọi người ơi, cíu iem vs ạ!
Đề: Tìm 1 động từ sau đó mở rộng thành cụm động từ có mở rộng cụm chỉ-vị?![]()

tham khảo:
-Câu có chủ ngữ là cụm C – V:
+ Những con ong vàng cần mẫn bay đi bay lại hút nhụy hoa.
+ Bà nội đi hội Gióng về chia quà cho các cháu.
– Câu có vị ngữ là cụm C – V:
+ Người mẹ ấy tay không lúc nào ngơi.
+ Quyển truyện này tranh ảnh rất đẹp
– Câu có phụ ngữ là cụm C -V:
+ Cả lớp đã làm xong bài tập thầy giáo vừa ra.
+ Hương lúa nếp đang trổ trên cánh đồng thấm vào hồn em mỗi sáng di đến trường.
+ Chúng tôi cũng không nhớ nó ăn hết bao nhiêu nải chuối, gồi lá
+ Bác mong các cháu mai sau lớn lên thành những người dân xứng đáng với nước độc lập, tự do.

The water isn't warm enough for me to drink
Homework is easy enough for me to do
He is rich enough to buy the car
She is intelligent enough to become the winner of the competition
Hoa is intelligent enough to become a genius
He isn't tall enough to take that book off the shelf
This shirt isn't cheap enough for me to buy
This dress isn't big enough for me to wear

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm


How you ( be ) ? => How are you
We ( be ) fine, thanks => We are fine, thanks
Theo mình thì không sai nhé
hok tốt
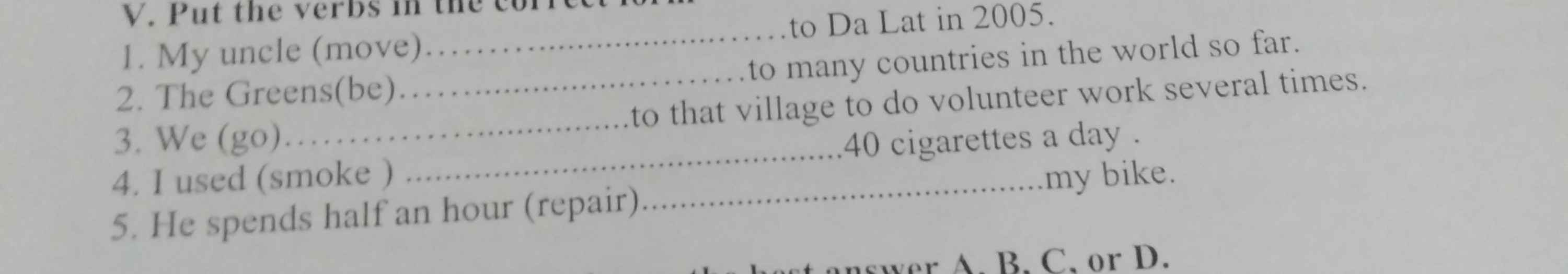



 Cíu t bài này với, gấp ạ:((
Cíu t bài này với, gấp ạ:(( giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !

cíu là chi
1.travelling ( enjoy + Ving)