Giải giúp mình Bài 1 với, nhanh nhanh nha, cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TH
1
Những câu hỏi liên quan
HK
1
LN
0
9 tháng 5 2021
a)Sau so thoi gian o to gap xe may la:
225 : ( 55 + 35 ) = 2,5 ( gio )
Doi : 2,5 gio = 2 gio 30 phut
b) Cho gap nhau cach a quang duong dai la:
55 x 2,5 = 137,5 ( km )
Dap so : a) 2 gio 30 phut
b) 137,5 km
9 tháng 5 2021
Gọi thời gian 2 xe gặp nhau là: T (giờ)
Quãng đường ô tô đi được là: 55 x T
Quãng đường xe máy đi được là: 35 x T
Mà tổng quãng đường là 225km
=> 55xT + 35xT =225
<=> 90xT=225
<=> T =2,5
Đổi 2,5 giờ = 2 giờ 30 phút
Vậy sau 2 giờ 30 phút thì 2 xe gặp nhau
Chỗ gặp cách A số km là : 55 x 2,5 = 137,5 (km)
Chúc em học tốt nhé!!!
3 tháng 10 2021
Bài 5:
Theo đề, ta có:
\(\left(2x+5\right)^2-4x^2-12x=41\)
\(\Leftrightarrow20x-12x=41+25=66\)
hay \(x=8.25\left(m\right)\)
Chu vi là:
\(\left[\left(2\cdot8.25+5\right)^2+\left(4\cdot8.25^2+12\cdot8.25\right)\right]\cdot2=1667\left(m\right)\)
TC
26 tháng 5 2022
\(M=\dfrac{10n+25}{2n+4}=\dfrac{5\left(2n+5\right)}{2n+4}=5\cdot\dfrac{2n+4}{2n+4}+\dfrac{1}{2n+4}\)
để M ∈ Z
=> \(2n+4\inƯ\left\{1\right\}=\left\{-1;1\right\}\)
\(=>\left\{{}\begin{matrix}2n+4=1\\2n+4=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=-3\\2n=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=-\dfrac{3}{2}\\n=-\dfrac{5}{2}\end{matrix}\right.\) thì M ∈Z
N
1
24 tháng 6
Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
AV
1
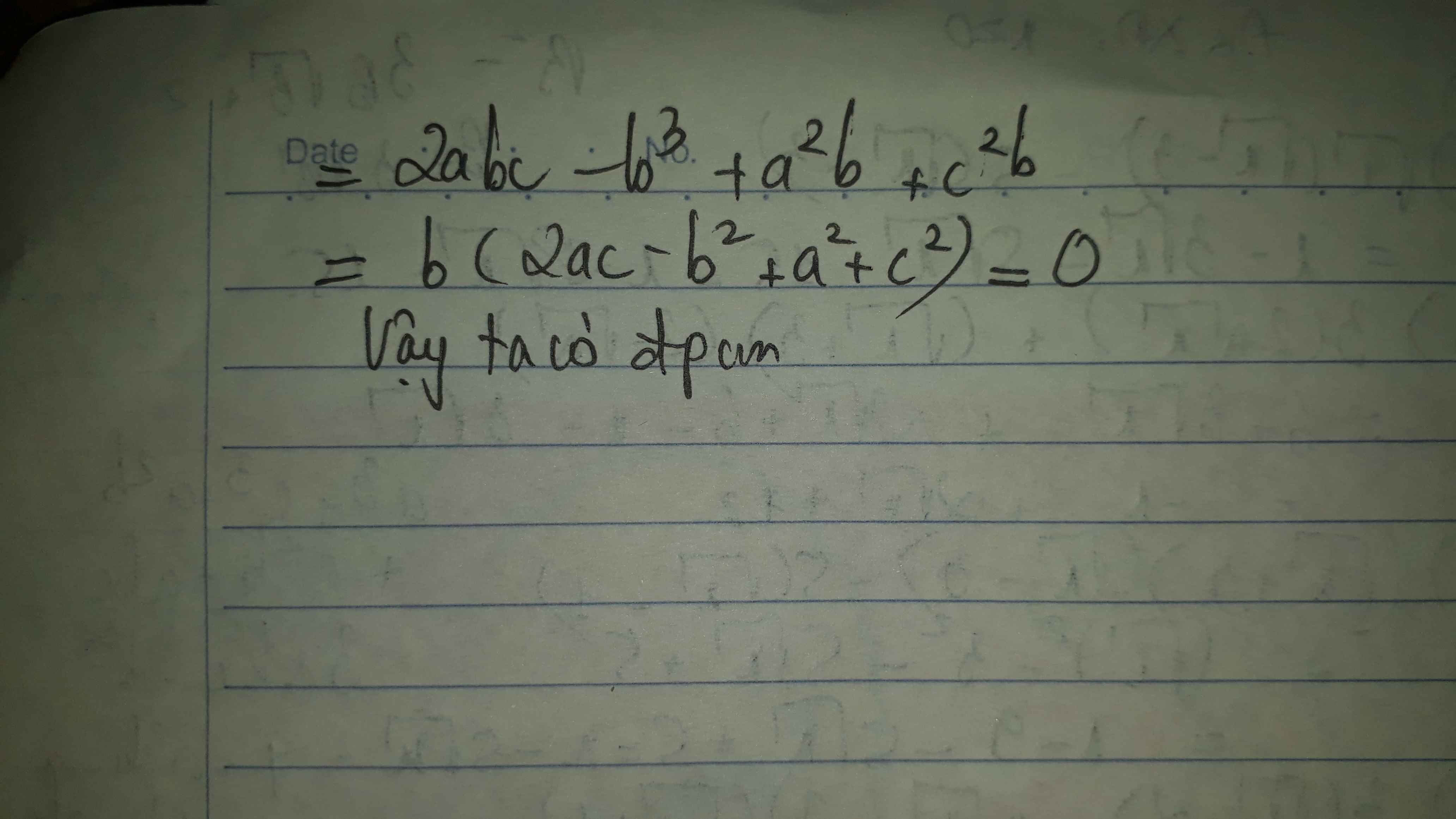
Bài 1:
Xét ΔDEF có
M là trung điểm của DE
P là trung điểm của DF
Do đó: MP là đường trung bình
=>MP//EF
=>ΔDMP\(\sim\)ΔDEF
Xét ΔDEF có
M là trung điểm của ED
N là trung điểm của FE
Do đó: MN là đường trung bình
=>ΔEMN\(\sim\)ΔEDF
Xét ΔDEF có
P là trung điểm của DF
N là trung điểm của EF
Do đó: PN là đường trung bình
=>PN//DE
hay ΔFPN\(\sim\)ΔFDE