Cho hình thang ABCD có 2 cạnh bên là AC và BD.Vẽ đường trung bình MN của hình thang đó.Chứng minh AB,MN,CD song song với nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
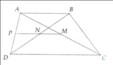

Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)

a:Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔDAB có
M là trung điểm của AD
ME//AB
Do đó: E là trung điểm của BD
Xét ΔABC có
N là trung điểm của BC
NF//AB
Do đó: F là trung điểm của AC

a: Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔADC có
M là trung điểm của AD
MF//DC
Do đó: F là trung điểm của AC
Xét ΔBDC có
N là trung điểm của BC
NE//DC
Do đó: E là trung điểm của BD
Nối AD,MD,BC,NC .Ta có :
SACD = 2SMCD (vì có chung đường cao hạ từ D và có đáy AC = 2MC)
SBCD = 2SNCD (vì có chung đường cao hạ từ C và có đáy BD = 2ND)
SACD = SBCD (vì có đường cao hạ từ A và B bằng nhau và có chung đáy CD)
=> SMCD = SNCD => Đường cao hạ từ M và N của 2 tam giác MCD và NCD bằng nhau (vì SMCD = SNCD và có chung đáy CD)
=> MN // CD mà AB // CD nên AB,MN,CD song song với nhau.