Tìm x,y biết 25 - y^2=8 . (x-2015)^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







Cách nhanh nhất để giải bài này là dùng phương pháp chặn em nhé.
Phương pháp chặn là giới hạn các giá trị của biến kết hợp điều kiện đề bài để tìm biến. Em tham khảo cách này của cô xem.
25 - y2 = 8( \(x\) - 2015)2
ta có: ( \(x-2015\))2 ≥ 0 ∀ \(x\) (1)
Mặt khác ta có: y2 ≥ 0 ∀ y ⇒ - y2 ≤ 0 ∀ y ⇒ 25 - y2 ≤ 25 ∀ y
⇒ 25 - y2 = 8(\(x-2015\))2 ≤ 25 ∀ \(x,y\)
⇒ (\(x-2015\))2 ≤ \(\dfrac{25}{8}\) = 3,125 ∀ \(x\) (2)
Kết hợp (1) và (2) ta có: 0 ≤ (\(x-2015\))2 ≤ 3,125
vì \(x\in\) Z nên ⇒ (\(x-2015\))2 \(\in\) Z
⇒ (\(x-2015\))2 \(\in\) {0; 1; 2; 3}
th1:(\(x-2015\) )2= 0 ⇒ \(x\) = 2015; ⇒ 25 - y2 = 0⇒ y = +-5
th2:(\(x-2015\))2 = 1⇒ 25 - y2 = 8 ⇒ y2 = 25 - 8 ⇒ y = +- \(\sqrt{17}\) ( loại)
th3: (\(x-2015\))2 = 2 ⇒ \(\left[{}\begin{matrix}x=\sqrt{2}+2015\left(ktm\right)\\x=-\sqrt{2}+2015\left(ktm\right)\end{matrix}\right.\)
th4: (\(x-2015\))2 = 3 ⇒ \(\left[{}\begin{matrix}x=\sqrt{3}+2015\left(ktm\right)\\x=-\sqrt{3}+2015\left(ktm\right)\end{matrix}\right.\)
Vậy (\(x,y\)) = ( 2015; -5); ( 2015; 5) là giá trị thỏa mãn đề bài

Ta có: (x - 2015)2 \(\ge\)0 \(\forall\)x => 8(x - 2015)2 \(\ge\)0 \(\forall\)x
=> 25 - y2 \(\ge\)0
<=> y2 \(\le\) 25
<=> |y| \(\le\)5
Do y \(\in\)Z => 0 \(\le\)y < 5
+) Với y = 0 => 25 - 02 = 8(x - 2015)2
=> 25 = 8(x - 2015)2
=> (x - 2015)2 = 25 : 8 (ko thõa mãn vì (x - 2015)2 là số chính phương còn 25 : 8 ko phải là số chính phương)
+)Với y = 1 => 25 - 12 = 8.(x - 2015)2
=> 24 = 8.(x - 2015)2
=> (x - 2015)2 = 24 : 8 = 3 (ko thõa mãn)
+) Với y = 2 => 25 - 22 = 8(x - 2015)2
=> 21 = 8(x - 2015)2
=> (x - 2015)2 = 21 : 8 (ko thõa mãn)
+) Với y = 3 => 25 - 32 = 8(x - 2015)2
=> 16 = 8(x - 2015)2
=> (x - 2015)2 = 16 : 8 = 2 (ko thõa mãn)
+) Với y = 4 => 25 - 42 = 8(x - 2015)2
=> 9 = 8(x - 2015)2
=> (x - 2015)2 = 9 : 8 (ko thõa mãn)
+) Với y = 5 => 25 - 52 = 8(x - 2015)2
=> 0 = 8(x - 2015)2
=> (x - 2015)2 = 0
=> x - 2015 = 0
=> x = 2015
Vậy {x;y} thõa mãn là {2015; 5}

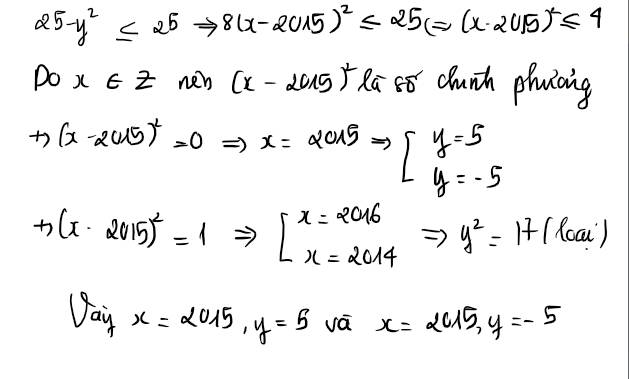
Ta có
25 - y^2 = 8(x-2009)^2
Dễ dàng thấy rằng vế phải luôn dương.Nên vế trái phải dương.Nghĩa là 25-y^2 >=0
Mặt khác do
8(x-2009)^2 chia hết cho 2.Như vậy Vế phải luôn chẳn
Do đó y^2 phải lẻ.( hiệu hai số lẽ là 1 số chẳn.hehe)
Do vậy chỉ tồn tại các giá trị sau
y^2 = 1, y^2 = 9, y^2 = 25
y^2 = 1; (x-2009)^2 = 3 (loại)
y^2 = 9; (x-2009)^2 = 2 (loại)
y^2 = 25; (x-2009)^2 = 0; x = 2009
Vậy có 2 cặp số x,y là: (2009 , -5) ; (2009 , 5)