Cho S.ABC, SA vuông góc với đáy. Tam giác ABC vuông tại A. Xác định góc tạo bởi SB và (SAC )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 2 2021
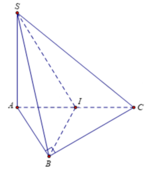
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)
CM
3 tháng 6 2019
Đáp án A
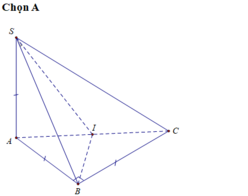
Gọi I là trung điểm của AC. Ta có: A I ⊥ S A C
Khi đó S B ; S A C = B S I ⏜
Đặt S A = A B = B C = a . . Ta có B I = a 2 2 ; S B = a 2
sin B S I ⏜ = B I S B = a 2 2 a 2 = 1 2 ⇒ B S I ⏜ = 30 °
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2023
a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
(SAB) và (SAC)