Cho (H) tiếp xúc trong với (O), gọi D là điểm tiếp xúc giữa hai đường tròn (DH < OD). Gọi A là điểm thuộc (O) ( A khác D) sao cho các tiếp tuyến AE, AF của (H) ( E,F là các tiếp điểm) cắt (O) lần lượt tại B và C thỏa AB < AC. Gọi P là giao điểm thứ hai của DF với (O).
a) Chứng minh PD là tia phân giác của góc ADC
b) Tia p.giác góc BDC cắt EF tại Q. Cm QFCD nội tiếp
c) Dm QD^2 = DB.DC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Theo tính chất hai tiếp tuyến giao nhau thì AE = AF
Có ^CDQ = ^BDC/2 = (1800 - ^BAC)/2 = ^AFE (Vì \(\Delta\)AEF cân tại A)
Suy ra tứ giác QFCD nội tiếp (đpcm).
+) Chứng minh tương tự ta có tứ giác DQEB nội tiếp
Do đó ^DCQ = ^DFQ = ^DEB = ^DQB. Kết hợp với ^QDC = ^BDQ
Suy ra \(\Delta\)DQC ~ \(\Delta\)DBQ (g.g). Vậy thì \(\frac{DQ}{DB}=\frac{DC}{DQ}\Rightarrow QD^2=DB.DC\)(đpcm).

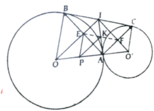
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’

a) Xét (O): AI và DI là 2 tiếp tuyến cắt nhau tại I (gt)
=> AI = DI (TC 2 tiếp tuyến cắt nhau)
CMTT: AI = EI (TC 2 tiếp tuyến cắt nhau)
=> AI = EI = DI
Mà DE = EI + DI
=>AI = EI = DI =\(\dfrac{DE}{2}\)
Xét tam giác ADE có: AI = EI = DI =\(\dfrac{DE}{2}\)(cmt)
=> Tam giác ADE vuông tại A (định lý đảo đường trung tuyến trong tam giác vuông)
=> ^MAN = 90o
Xét tam giác AID: AI = DI (cmt) => Tam giác AID cân tại I
Mà IM là đường phân giác AID (AI và DI là 2 tiếp tuyến cắt nhau tại I)
=> IM là đường cao
=> ^IMA = 90o
CMTT: ^ANI = 90o
Xét TG AMIN:
^IMA = 90o (cmt)
^ANI = 90o (cmt)
^MAN = 90o (cmt)
=> AMIN là hình chữ nhật (dhnb)
b) Xét tam giác OAI vuông tại A, AM là đường cao ( do AM vg góc OI)
=> IM.IO = IA2 (HTL) (1)
Xét tam giác O'AI vuông tại A, AN là đường cao ( do AN vg góc O'I)
=> IN.IO' = IA2 (HTL) (2)
Từ (1) và (2) => IM.IO = IN.IO’ (đpcm)
c) Xét (O) và (O'): 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A (cmt)
=> A \(\in\)OO' (TC đường nối tâm)
mà IA vg góc AO (do AI là tiếp tuyến trong của 2 đường tròn (O) và (O’) tiếp xúc ngoài tại A )
=> OO' vg góc AI tại A (*)
Xét tam giác ADE vuông tại A (^DAE = 90o do AMIN là hcn)
I là TĐ của DE (do ID = IE = \(\dfrac{DE}{2}\))
=> I là tâm đường tròn đường kính DE, nội tiếp tam giác ADE
=> A \(\in\)(I) (**)
Từ (*) và (**) => OO’ là tiếp tuyến của đường tròn đường kính DE có A là tiếp điểm.
d) Xét tg OIO' vuông tại I, AI là đường cao:
AI2 = AO . AO' (HTL)
=> AI2= R. R'
Mà AI = \(\dfrac{DE}{2}\)(cmt)
=> (\(\dfrac{DE}{2}\))2 = R . R'
<=> \(\dfrac{DE^2}{4}\) = R . R'
<=> DE = 2\(\sqrt{R.R'}\)

a: ΔOED cân tại O
mà OF là trung tuyến
nên OF vuông góc ED
=>OF vuông góc EA
góc OFA=góc OBA=góc OCA=90 độ
=>O,F,C,A,B cùng thuộc 1 đường tròn
b: Xét ΔICD và ΔIBC có
góc ICD=góc IBC
góc CID chung
=>ΔICD đồng dạng với ΔIBC
=>IC/IB=ID/IC
=>IC^2=IB*ID
Xét ΔIAD và ΔIBA có
góc IDA=góc IAB
góc AID chung
=>ΔIAD đồng dạng với ΔIBA
=>IA/IB=ID/IA
=>IA^2=IB*ID
=>IA=IC
=>I là trung điểm của AC

a, Theo t/c tiếp tuyến của đường tròn
EA = EC
FC = FB
=> EC + CF = EA + BF
=> EF = AE + BF
b, Xét \(\Delta\)ABC có OA = OB = OC (bán kính)
=> \(\Delta\)ABC vuông tại C
=> AC \(\perp\)BC
Xét \(\Delta\)DAB vuông tại A có AC là đường cao
=> \(AD^2=DC.DB\)(Hệ thức lượng)
c,Chưa ra, mai nghĩ ra thì giải cho ^^
sorry