Cho hai đường thẳng (d) : y = -x + m + 2 và (d') : y = (m2 - 2)x + 3.
Tìm m để (d) và (d') song song với nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để hai đường thẳng (d) và (d’) song song với nhau thì: − 1 = m 2 − 2 m + 2 ≠ 3 ⇔ m 2 = 1 m ≠ 1 ⇔ m = ± 1 m ≠ 1 ⇔ m = − 1
Vậy m = -1 là giá trị cần tìm.

Đáp án C
+Với m=1 ta có d: y=1 và d’: y=6
do đó hai đường thẳng này song song với nhau.
+ Với m =-1 ta có d: y= -2x-1 và d’: y= 6
suy ra hai đường thẳng này cắt nhau tại M(-7/2; 6)
+ Với m ≠ ± 1 khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi:
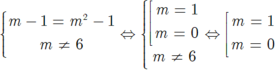
Đối chiếu với điều kiện m≠± 1 suy ra m= 0.
Vậy m= 0 và m= 1 là giá trị cần tìm.
Chọn C.

Để 2 đường thẳng d và d' song song với nhau thì
\(\left\{{}\begin{matrix}m^2-3m+5=m+2\\m-1\ne5-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+3=0\\2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(m-3\right)=0\\m\ne3\end{matrix}\right.\)
\(\Leftrightarrow m=1\left(tm\right)\)

a: Để (d)//(d') thì \(\left\{{}\begin{matrix}k-2=2\\-k\ne4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}k=4\\k\ne-4\end{matrix}\right.\)
=>k=4
b: Để (d) vuông góc (d') thì \(2\left(k-2\right)=-1\)
=>2k-4=-1
=>2k=3
=>\(k=\dfrac{3}{2}\)
c: Để (d) cắt (d') thì \(k-2\ne2\)
=>\(k\ne4\)

a: 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)