Tìm x ∈ ℕ biết:
9x = 9
x =
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
14 tháng 10 2023
Tìm x ∈ N
a) 2x chia hết cho 12 ⇒ 2x ∈ B(12)
2x chia hết cho 30 ⇒ 2x ∈ B(30)
Mà x có hai chữ số ⇒ 10 ≤ x ≤ 99
\(\Rightarrow2x\in BC\left(12;30\right)\)
Mà: \(B\left(12\right)=\left\{0;12;24;36;48;60;72;84;96;108;...\right\}\)
\(B\left(30\right)=\left\{0;30;60;90;120;...\right\}\)
\(\Rightarrow BC\left(12;30\right)=\left\{0;60;...\right\}\)
\(\Rightarrow2x=60\)
\(\Rightarrow x=\dfrac{60}{2}\\ \Rightarrow x=30\)
b) \(9^{x+2}-9^{x+1}+9^x=657\)
\(\Rightarrow9^x\cdot\left(9^2-9+1\right)=957\)
\(\Rightarrow9^x\cdot\left(81-8\right)=657\)
\(\Rightarrow9^x\cdot73=657\)
\(\Rightarrow9^x=9\)
\(\Rightarrow9^x=9^1\)
\(\Rightarrow x=1\)
14 tháng 10 2023
bạn có thể giải giùm mk bài tính nhanh đc ko??? Mk đang cần gấp á. Cảm ơn bạn nhiều nha!
T
7 tháng 1 2019
a)\(4x^3-9x=0\Leftrightarrow x\left(4x^2-9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\4x^2-9=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=\frac{9}{4}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)
Vậy x = 0 hoặc \(x=\frac{3}{2}\)
b) \(x^3+8x=0\Leftrightarrow x\left(x^2+8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x^2+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=-8\left(L\right)\end{cases}}\)
Vậy x = 0
c) \(-x^3+9x=0\Leftrightarrow x\left(-x^2+9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}-x^2+9=0\\x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2=9\\x=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=0\end{cases}}\)
Vậy ...
CM
21 tháng 7 2018
điều kiện: x - 1 ≥ 0 ⇔ x ≥ 1 (*)
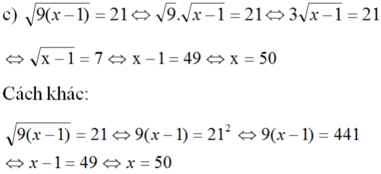
x = 50 thỏa mãn điều kiện (*) nên x = 50 là nghiệm của phương trình.
N
29 tháng 8 2021
\(5x^2-9x-2=0\)
\(\Delta=9^2-4.5.\left(-2\right)=121\)
\(\left[{}\begin{matrix}x_1=\dfrac{9+\sqrt{121}}{2.5}=2\\x_2=\dfrac{9-\sqrt{121}}{2.5}=-\dfrac{1}{5}\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 10 2023
\(3^{x+1}=9^x\\ \Leftrightarrow3^{x+1}=3^{2x}\\ \Leftrightarrow x+1=2x\\ \Leftrightarrow x=1\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 10 2023
\(VP=9^x=\left(3^2\right)^x=3^{2x}\\ Vì:3^{x+1}=9^x=3^{2x}\\ Nên:x+1=2x\\ \Rightarrow2x-x=1\\ Vậy:x=1\)
TL
1
28 tháng 3 2015
Để F(x) có nghiệm <=> x^10 - 9x^9 + ... + 9x^2 - 9x +8 = 0
<=> (x^10 - x^9) - (8x^9 - 8x^8) + (x^8 - x^7) - ... + (x^2 - x) - (8x - 8) = 0
<=> x^9(x - 1) - 8x^8(x - 1) + ... + x(x - 1) - 8(x - 1) = 0
<=> (x^9 - 8x^8 + ... + x - 8)(x - 1) = 0
<=> ( (x^9 - 8x^8) + (x^7 - 8x^6) + ... + (x - 8) )(x - 1) = 0
<=> (x^8 + x^6 + ... + 1)(x - 8)(x - 1) = 0
Có nghiệm là 8 và 1
4 tháng 8 2021
Ta có: \(x^3+6x^2+9x=0\)
\(\Leftrightarrow x\left(x+3\right)^2=0\)
hay \(x\in\left\{0;-3\right\}\)
8 tháng 12 2023
\(\left(5-x\right)\left(9x^2-4\right)=0\)
=>\(\left(x-5\right)\left(3x-2\right)\left(3x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-5=0\\3x-2=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
T
8 tháng 12 2023
\(\left(5-x\right)\left(9x^2-4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5-x=0\\9x^2-4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\x^2=\dfrac{4}{9}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
KB
31 tháng 3 2022
\(\left|x^3+x\right|-\left|9x^2+9\right|=0\)
\(\Leftrightarrow\left|x\left(x^2+1\right)\right|-9\left|x^2+1\right|=0\)
\(\Leftrightarrow\left(\left|x\right|-9\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\left|x\right|=9\left(x^2+1\ge1>0\right)\Leftrightarrow x=\pm9\)
Vậy ...
31 tháng 3 2022
\(\left|x^3+x\right|-\left|9x^2+9\right|=0\)
\(TH1:\left\{{}\begin{matrix}\left|x^3+x\right|=0\\\left|9x^2+9\right|=0\end{matrix}\right.\)
\(\text{Vì }9x^2\ge0\)
\(\Rightarrow9x^2+9\ge9\)
\(TH2:\left|x^3+x\right|=\left|9x^2+9\right|\)
\(\Rightarrow\left[{}\begin{matrix}x^3+x=9x^2-9\\x^3+x=9x^2+9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^3+x+9x^2+9=0\\x^3+x-9x^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x.\left(x^2+1\right)+9.\left(x^2+1\right)=0\\x.\left(x^2+1\right)-9.\left(x^2+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=9\end{matrix}\right.\)
9 tháng 7 2023
=>|x^3+x|=|9x^2+9|
=>x^3+x=9x^2+9 hoặc x^3+x=-9x^2-9
=>x^3-9x^2+x-9=0 hoặc x^3+9x^2+x+9=0
=>x+9=0 hoặc (x-9)(x^2+1)=0
=>x=9 hoặc x=-9
vì số nào mũ 1 cx = chính nó => x=1
x = 1 nha