giải hệ phương trình sau
(1) x3 + 1 =2y
(2) y3 + 1 =2X
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 9 2019
Cách 1
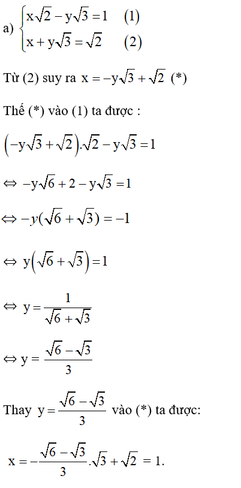
Vậy hệ phương trình có nghiệm duy nhất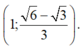 
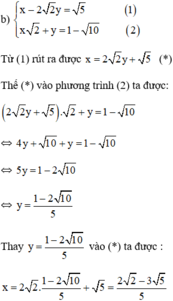
Vậy hệ phương trình có nghiệm duy nhất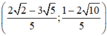 
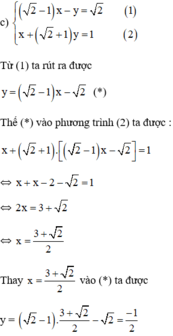
Vậy hệ phương trình có nghiệm duy nhất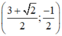 
Cách 2
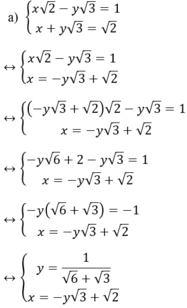
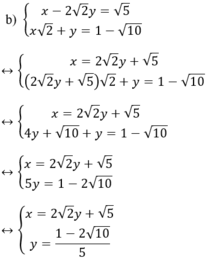
Kiến thức áp dụng
Giải hệ phương trình ta làm như sau:
Bước 1: Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
CM
16 tháng 10 2019
x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).
CM
11 tháng 5 2018
Lấy phương trình (2) trừ phương trình (1), vế trừ vế ta được:
Vậy hệ phương trình có nghiệm duy nhất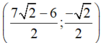 
Lưu ý:
TN
0
4 tháng 4 2022
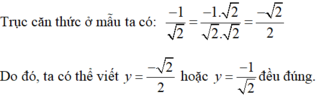
\(1,\dfrac{x-1}{3}=x+1\\ \Leftrightarrow x-1=3x+3\\ \Leftrightarrow3x-x=3+1\\ \Leftrightarrow x=2\)
PT có tập nghiệm S = {2}
\(2,\sqrt{16x^2+8x+1}-2=x\\ \Leftrightarrow\sqrt{\left(4x+1\right)^2}-2=x\\\Leftrightarrow 4x+1-2=x\\ \Leftrightarrow4x-x=2-1\\ \Leftrightarrow x=\dfrac{1}{3}\)
PT có tập nghiệm S = {1/3}
\(3,\left\{{}\begin{matrix}2x+y=17\\x-2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=17\\2x-4y=2\end{matrix}\right.\\ \Leftrightarrow\left(2x+y\right)-\left(2x-4y\right)=17-2\\ \Leftrightarrow5y=15\\ \Leftrightarrow y=3\\ \Leftrightarrow2x+3=17\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\)
PTHH có tập nghiệm (x; y) là (7; 3)
\(\hept{\begin{cases}x^3+1=2y\left(1\right)\\y^3+1=2x\left(2\right)\end{cases}}\) Lấy (1) trừ (2) theo vế ta được :
\(x^3+1-y^3-1=2y-2x\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)=-2\left(x-y\right)\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2+2\right)=0\)
=> \(x-y=0\)hoặc \(x^2+xy+y^2+2=0\)
Ta có : \(x^2+xy+y^2+2=0\Leftrightarrow2x^2+2xy+2y^2+4=0\Leftrightarrow\left(x+y\right)^2+x^2+y^2+4=0\)
Vì \(\left(x+y\right)^2+x^2+y^2+4\ge4>0\). Do đó dấu đẳng thức không xảy ra.
Ta xét x = y thay vào (1) được : \(x^3+1=2x\)
Giải phương trình trên ta được : \(x=1\)hoặc \(x=-\frac{1}{2}-\frac{\sqrt{5}}{2}\) hoặc \(x=-\frac{1}{2}+\frac{\sqrt{5}}{2}\)
Vậy : Nghiệm của hệ là : \(\left(x;y\right)=\left(1;1\right);\left(-\frac{1}{2}-\frac{\sqrt{5}}{2};-\frac{1}{2}-\frac{\sqrt{5}}{2}\right);\left(-\frac{1}{2}+\frac{\sqrt{5}}{2};-\frac{1}{2}+\frac{\sqrt{5}}{2}\right)\)
chuyển vế t đc hệ pt
x^3 -2y+1=0
y^3-2x+1=0
rồi hạ bậc xuống giải bt nhé