Cho tam giác ABC vuông cân tại A, có BC = a. Một đường thẳng d đi qua A. Từ B và C kẻ BH và CE vuông góc với d (H và E thuộc d). Tính BH2 + CE2 theo a.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 5 2015
Đường thẳng d bất kì đi qua A nên d có thể có các vị trí sau:
+) d không cắt cạnh BC.
Trong tam giác vuông AHB có: góc HAB + ABH = 900 (1)
Mà góc HAB + BAC + CAE = 180o => góc HAB + CAE = 180o - BAC = 180 - 90 = 90o (2)
(1)(2) => góc ABH = CAE
tam giác vuông ABH = CAE ( do cạnh huyền AB = AC; góc ABH = CAE)
=> AH = CE
*) Áp dụng định lí Pi ta go trong tam giác vuông ABH có: BH2 + AH2 = AB2
mà AH = CE nên BH2 + CE2 = BH2 + AH2 = AB2
Dễ có: AB2 + AC2 = BC2 ; AB = AC => 2.AB2 = a2 => AB2 = a2/ 2
Vậy BH2 + CE2 = a2/ 2
+) Khi d trùng với AB :
=> H trùng với B; E trùng với A=> BH = 0; CE = CA
=> BH2 + CE2 = AC2 = a2/ 2
+) d trùng với AC (tương tự như d trùng với AB)
+) Khi d cắt cạnh BC:
*) Ta cũng chứng minh : tam giác AEC = BHA (cạnh huyền - góc nhọn)
=> BH = AE
*) Trong tam giác vuông AEC có: AE2 + CE2 = AC2
=> BH2 + CE2 = AE2 + CE2 = AC2 = a2/ 2
Vậy BH2 + CE2 = AC2 = a2/ 2
31 tháng 12 2020
Mình nghĩ M là trung điểm của BC.
Xét tam giác MAE và tam giác MBD có: MA = MB (do tam giác ABC vuông cân tại A), AE = BD (chứng minh trên), \(\widehat{MBD}=\widehat{MAE}\).
Do đó \(\Delta MAE = \Delta MBD(c.g.c)\Rightarrow MD=ME; \widehat{AME}=\widehat{BMD})\Rightarrow MD=ME; \widehat{EMD}=\widehat{AMB}=90^o\Rightarrow\text{Tam giác MDE vuông cân tại M}\).
31 tháng 12 2020
Ta có \(\Delta ADB=\Delta CEA\left(g.c.g\right)\)
\(\Rightarrow BD=EA\).
Do đó \(BD^2+CE^2=EA^2+CE^2=AC^2\) không đổi.
CG
24 tháng 1 2017
CO TAM GIAC ABC CAN TAI A
=>AB=AC( DN TAM GIÁC CÂN)
SUY RA GÓC ABC = GÓC ACB( DN TAM GIÁC CÂN)
CÓ GÓC ABC VÀ GÓC ABD LÀ 2 GÓC KỀ BÙ
SUY RA GÓC ABD+ GÓC ABC = 180 ĐỘ
CÓ GÓC ACB VÀ GÓC ACE LÀ 2 GÓC KỀ BÙ
SUY RA GÓC ACB + GÓC ACE = 180 ĐỘ
MÀ GÓC ABC = GÓC ACB( CMT)
SUY RA GÓC ABD+ GÓC ABC = GÓC ACB + ACE( =180 ĐỘ)
=> GÓC ABD= GÓC ACE
XÉT TAM GIÁC ADB VÀ TAM GIÁC AEC CÓ:
AB=AC( CMT)
GÓC ABD = GỐC ACE ( GMT)
DB=EC( GT)
=> TAM GIÁC ADB = TAM GIÁC AEC( C-G-C)
=>AD=AE( 2 CẠNH TƯƠNG ỨNG)
=> TAM GIAC ADE CAN TAI A( DN TAM GIAC CAN)
b)CÓ TAM GIÁC ADE CÂN TẠI A( CMT)
=>GÓC D = GÓC E( ĐN TAM GIÁC CÂN)
CÓ M LÀ TRUNG ĐIỂM CỦA BC=>BM=CM
CO ME = MC+CE
MD=MB+BD
MA CE=BD
MB=MC
=>MD=ME
XÉT TAM GIÁC AMD VÀ TAM GIÁC AME CÓ:
AD= AE(CM CÂU a)
GÓC D=GÓC E(CMT)
MD=ME( CMT)
SUY RA TAM GIÁC AMD= TAM GIÁC AME( C-G-C)
=>GÓC ĐAM = GÓC EAM( 2 GÓC TƯƠNG ỨNG)
SUY RA AM LÀ TIA PHÂN GIÁC CỦA GÓC DAE
CÓ TAM GIÁC AMD = TAM GIÁC AME
SUY RA GÓC AMD = GÓC AME( 2 GÓC TƯƠNG ỨNG)
MÀ 2 GÓC NÀY LÀ 2 GÓC KỀ BÙ
SUY RA AMD+AME = 180 ĐỘ
CÓ GÓC AMD = GÓC AME = 180 ĐỘ :2 = 90 ĐỘ
SUY RA AM VUONG GOC VS DE
CHO BN 2 CAU TRC LAM NAY
NHO K CHO MINH NHA
CG
24 tháng 1 2017
CO TAM GIAC ADM = TAM GIAC ACE( CM O CAU A)
SUY RA GÓC DAB = GÓC EAC( 2 GÓC TƯƠNG ỨNG)
XÉT TAM GIC AHB VUÔNG TẠI H VÀ TAM GIÁC AKC VUÔNG TẠI K CÓ:
AB = AC ( CM Ở CÂU a)
GÓC DAB = GÓC EAC ( CMT)
=> TAM GIÁC AHB = TAM GIÁC AKC( CH-GN)
=> BH = CK( 2 CẠNH TƯƠNG ỨNG)
d)KHI NÀO MÌNH NGHĨ XONG MÌNH SẼ NS CHO CẬU
2
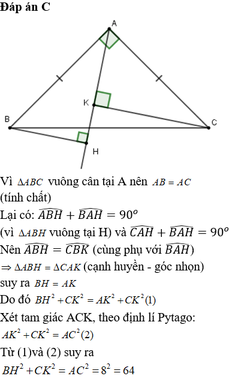
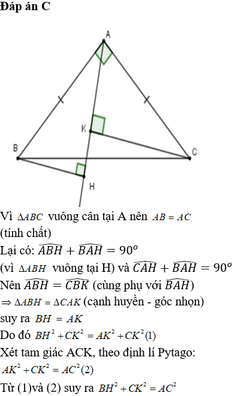
Đường thẳng d bất kì đi qua A nên d có thể có các vị trí sau:
+) d không cắt cạnh BC.
Trong tam giác vuông AHB có: góc HAB + ABH = 900 (1)
Mà góc HAB + BAC + CAE = 180o => góc HAB + CAE = 180o - BAC = 180 - 90 = 90o (2)
(1)(2) => góc ABH = CAE
tam giác vuông ABH = CAE ( do cạnh huyền AB = AC; góc ABH = CAE)
=> AH = CE
*) Áp dụng định lí Pi ta go trong tam giác vuông ABH có: BH2 + AH2 = AB2
mà AH = CE nên BH2 + CE2 = BH2 + AH2 = AB2
Dễ có: AB2 + AC2 = BC2 ; AB = AC => 2.AB2 = a2 => AB2 = a2/ 2
Vậy BH2 + CE2 = a2/ 2
+) Khi d trùng với AB :
=> H trùng với B; E trùng với A=> BH = 0; CE = CA
=> BH2 + CE2 = AC2 = a2/ 2
+) d trùng với AC (tương tự như d trùng với AB)
+) Khi d cắt cạnh BC:
*) Ta cũng chứng minh : tam giác AEC = BHA (cạnh huyền - góc nhọn)
=> BH = AE
*) Trong tam giác vuông AEC có: AE2 + CE2 = AC2
=> BH2 + CE2 = AE2 + CE2 = AC2 = a2/ 2
Vậy BH2 + CE2 = AC2 = a2/ 2