\(x^2:\left(x-3\right)\)
giúp mik vs, đặt tính chia vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(3x-\dfrac{2}{5}=0=>3x=\dfrac{2}{5}=>x=\dfrac{2}{15}\)
b)\(\left(x-3\right)\left(2x+8\right)=0=>\left[{}\begin{matrix}x-3=0\\2x=-8\end{matrix}\right.=>\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
c)\(3x^2-x-4=0=>3x^2+3x-4x-4=0=>\left(3x-4\right)\left(x+1\right)=0\)
\(=>\left[{}\begin{matrix}3x=4\\x+1=0\end{matrix}\right.=>\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=-1\end{matrix}\right.\)

Đây nè bạn. Mk chỉ mới nghĩ ra cách này thôi à!!! Bạn nào có cách nào thì bảo mk với nhé!!!
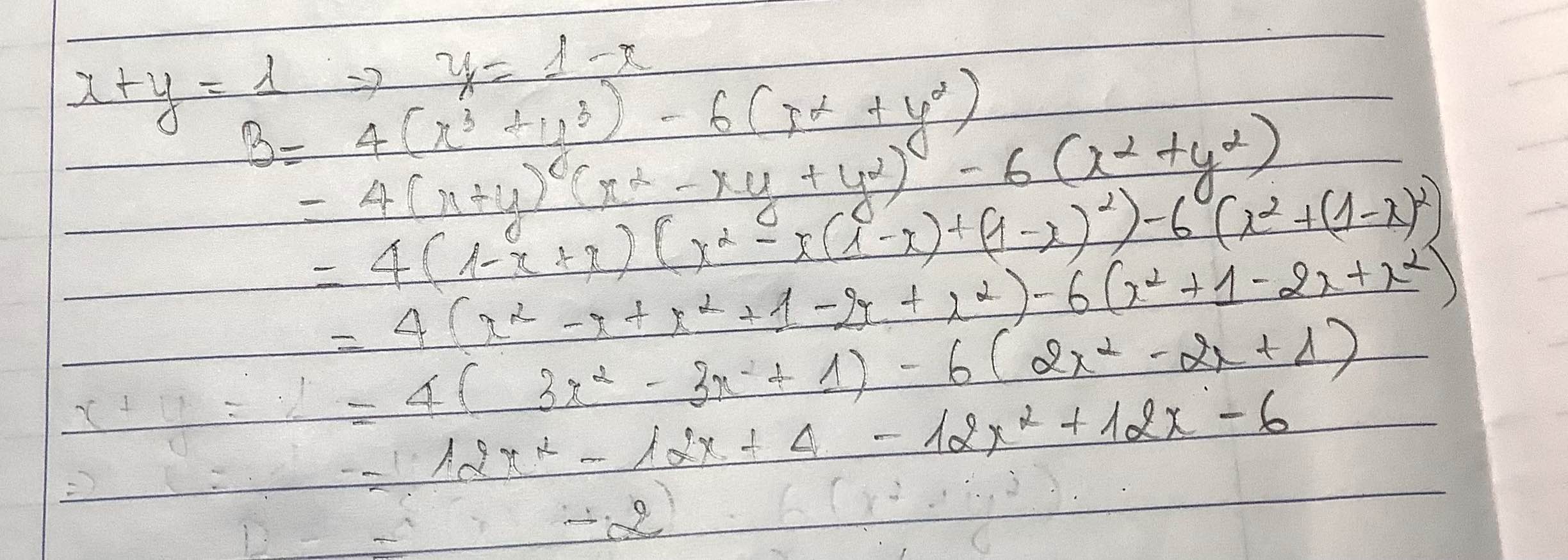
\(B=4\left(x+y\right)\left(x^2+y^2-xy\right)-6\left[\left(x+y\right)^2-2xy\right]\)
\(=4\left[\left(x+y\right)^2-3xy\right]-6\left(1-2xy\right)\)
\(=4-12xy-6+12xy\)
\(=-2\)

\(A=\frac{x^2}{\left(x-y\right)\left(x-z\right)}+\frac{y^2}{\left(y-x\right)\left(y-z\right)}+\frac{z^2}{\left(z-x\right)\left(z-y\right)}\)
\(=\frac{x^2}{\left(x-y\right)\left(x-z\right)}-\frac{y^2}{\left(x-y\right)\left(y-z\right)}+\frac{z^2}{\left(x-z\right)\left(y-z\right)}\)
\(=\frac{x^2\left(y-z\right)-y^2\left(x-z\right)+z^2\left(x-y\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(x^2\left(y-z\right)-y^2\left(x-z\right)+z^2\left(x-y\right)\)
\(=x^2y-x^2z-xy^2+y^2z+z^2\left(x-y\right)\)
\(=xy\left(x-y\right)-z\left(x-y\right)\left(x+y\right)+z^2\left(x-y\right)\)
\(=\left(x-y\right)\left[xy-zx-zy+z^2\right]\)
\(=\left(x-y\right)\left[x\left(y-z\right)-z\left(y-z\right)\right]=\left(x-y\right)\left(x-z\right)\left(y-z\right)\)
Vậy A = 1

ĐK: \(x,y\ge0\)
\(hpt\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x}-2\sqrt{y}=-2\left(1\right)\\4\sqrt{x}+2\sqrt{y}=2\end{matrix}\right.\)
Cộng vế theo vế 2 phương trình ta được: \(7\sqrt{x}=0\Leftrightarrow x=0\)
Khi đó \(\left(1\right)\Leftrightarrow-2\sqrt{y}=-2\Leftrightarrow y=1\)
Vậy hệ đã cho có nghiệm \(\left(x;y\right)=\left(0;1\right)\)
ĐKXĐ: \(x\ge0;y\ge0\)
\(\left\{{}\begin{matrix}3\sqrt{x}-2\sqrt{y}=-2\\2\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x}-2\sqrt{y}=-2\\4\sqrt{x}+2\sqrt{y}=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x}=0\\2\sqrt{x}+\sqrt{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2\sqrt{0}+\sqrt{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\0+\sqrt{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\\sqrt{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\) (TM)
Vậy...

\(\left(x+1\right)\left(x+2\right)\left(x+3\right)-x^3-8x\left(x+2\right)=6\\ \Leftrightarrow\left(x^2+3x+2\right).\left(x+3\right)-x^3-8x^2-16x=6\\ \Leftrightarrow x^3+6x^2+11x+6-x^3-8x^2-16x-6=0\\ \Leftrightarrow-2x^2-5x=0\\ \Leftrightarrow x.\left(-2x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\-2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

ĐK: x\(\ne\){-3;0;3}.
\(\dfrac{x^2-3x}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{3x^2}=\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{3x^2}=\dfrac{1}{3x}\).
\(x^2:\left(x-3\right)\left(đk:x\ne3\right)\)
\(=x^2:x-x^2:3\)
\(=x-\dfrac{x^2}{3}\)