Cho tam giác ABC có M là trung điểm BC. Từ M kẻ các đường thẳng song song với AB, AC cắt AC, AB lần lượt tại N, P. Chứng minh:PA = PB, PN song song với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2022
a: Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
hay PA=PB
b: Xét ΔABC có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
P là trung điểm của AB
N là trung điểm của AC
Do đó: PN là đường trung bình
=>PN//BC
LV
25 tháng 2 2022
Cô ơi! bài này hình lớp 7 có áp dụng đường trung bình được hôn Co.
30 tháng 11 2016
Xét \(\Delta ABC:\)N là trung điểm AC, P là trung điểm BC
\(\Rightarrow NP\)là đường trung bình \(\Delta ABC\)
\(\Rightarrow NP\text{//}AB\)
\(\Rightarrow PQ\text{//}AM\)( Vì \(M\in AB;N\in PQ\))
\(\Rightarrow\)Tứ giác PMAQ là hình thang
Vậy...
25 tháng 8 2021
(Tự vẽ hình)
Do BM//NI, MN//BI nên MNIB là hình bình hành
=> BM=IN (2 cạnh đối) (1)
Trong tam giác ABC, do M trung điểm AB, MN//BC => N trung điểm AC (2)
Do MA=MB,NA=NC nên MN là đường trung bình tam giác ABC => MN=1/2 BC (4)
CMTT, ta có I trung điểm BC (3)
Vậy ta có tất cả đpcm
15 tháng 7 2021
a) Xét ΔAMN và ΔCND có
\(\widehat{MAN}=\widehat{NCD}\)(hai góc so le trong, AB//CD)
AN=NC(N là trung điểm của AC)
\(\widehat{ANM}=\widehat{CND}\)(hai góc đối đỉnh)
Do đó: ΔAMN=ΔCND(g-c-g)
b) Xét ΔABC có
M là trung điểm của BA(gt)
N là trung điểm của AC(Gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC
15 tháng 7 2021
a) Xét ΔAMN và ΔCND có
\(\widehat{MAN}=\widehat{NCD}\)(hai góc so le trong, AB//CD)
AN=NC(N là trung điểm của AC)
\(\widehat{ANM}=\widehat{CND}\)(hai góc đối đỉnh)
Do đó: ΔAMN=ΔCND(g-c-g)
b) Xét ΔABC có
M là trung điểm của BA(gt)
N là trung điểm của AC(Gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra:MN//BC
21 tháng 12 2022
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>MF=ME
=>M là trung điểm của EF
=>BD=CE
12 tháng 5 2023
MP/AD=BP/BD=BM/AB
=>MP*BD=BP*AD
AD/NP=CD/CP
=>AD*CP=NP*CD
=>MP*BD+CD*NP=BP*AD+AD*CP
=>MP+NP=2AD
=>PM+PN ko đổi
KV
16 tháng 12 2023
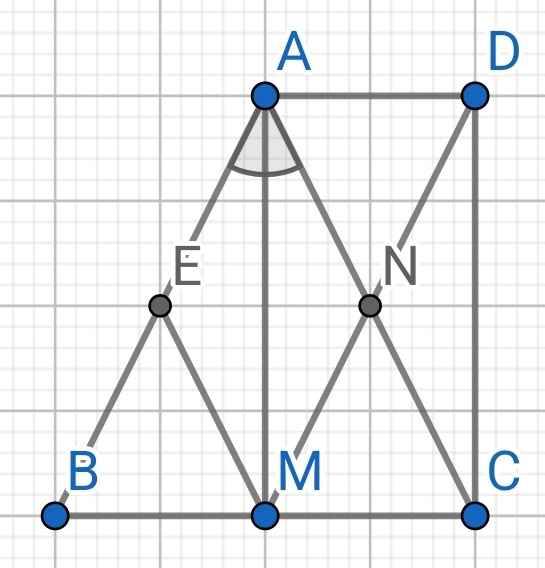a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành
Xét ΔABC có
M là trung điểm của BC
MP//AC
Do đó: P là trung điểm của AB
hay PA=PB
Xét ΔABC có
M là trung điểm của BC
MN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
P là trung điểm của AB
N là trung điểm của AC
DO đó: PN là đường trung bình
=>PN//BC