7x(3-x)-12x(x-5)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PL
4 tháng 3 2020
-12x(x - 5) + 7x(3 - x) = 5
-12x2 + 60 + 21x - 7x2 = 5
-19x2 + 21x + 60 - 5 = 0
-19x2 + 21x + 55 = 0
\(\Delta=b^2-4ac=21^2-4.55.\left(-19\right)=441+4180=4621>0\)
vậy phtrinh có hai nghiệm phân biệt:
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-21+\sqrt{4621}}{2.\left(-19\right)}=\frac{-21+\sqrt{4621}}{-38}\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-21-\sqrt{4621}}{2.\left(-19\right)}=\frac{-21-\sqrt{4621}}{-38}\)
4 tháng 3 2020
\(-12x\left(x-5\right)+7x\left(3-x\right)=5\)
\(-12x^2+60+21x-7x^2=5\)
\(-19x^2+60+21x=5\)
\(-19x^2+21x=5-60=-55\)
\(-19x^2+21x+55=0\)
\(a=-19;b=-21;c=55\)
\(=B^2-4ac\)
\(=21^2-4\left(-19\right).55\)
\(\Delta=4621\)
Giá trị delta cao hơn 0, vì vậy pt có hai nghiệm
\(x_1=\frac{-b-\sqrt{\Delta}}{2a};x_2=\frac{-b+\sqrt{\Delta}}{2a}\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{\left(-21\right)-\sqrt{4621}}{2.\left(-19\right)}=\frac{-21-\sqrt{4621}}{-38}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-21+\sqrt{4621}}{2.\left(-19\right)}=\frac{-21+\sqrt{4621}}{-38}\)
15 tháng 1 2017
a) \(^{x^3}\) - 7x+6=0
\(\Leftrightarrow\) \(^{x^3}\) - x-6x+6=0
\(\Leftrightarrow\) \(\left(x^3-x\right)\) - \(\left(6x-6\right)\) =0
\(\Leftrightarrow\) x\(\left(x^2-1\right)\) - 6\(\left(x-1\right)\) =0
\(\Leftrightarrow\) x\(\left(x+1\right)\)\(\left(x-1\right)\) - 6\(\left(x-1\right)\) =0
\(\Leftrightarrow\) \(\left(x-1\right)\) \(\left[x-6\left(x+1\right)\right]\) =0
\(\Leftrightarrow\) \(\left(x-1\right)\) \(\left(6-5x\right)\) =0
\(\Leftrightarrow\) \(\left[\begin{matrix}x-1=0\\6-5x=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[\begin{matrix}x=1\\5x=-6\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left[\begin{matrix}x=1\\x=-\frac{6}{5}\end{matrix}\right.\)
Những câu sau dùng phương pháp phân tích đa thức thành nhân tử nhé!
22 tháng 2 2018
\(-12.\left(x-5\right)+7.\left(3-x\right)=5\)
\(\Rightarrow-12x+60+21-7x=5\)
\(\Rightarrow-12x-7x=5-60-21\)
\(\Rightarrow-19x=-76\)
\(\Rightarrow x=4\)
Vậy x = 4
22 tháng 2 2018
-12x(X-5)+7x(3-X)=5-12x(X-5)+7x(3-X)=5-12x(X-5)+7x(3-X)=5
ND
28 tháng 2 2018
b. sửa đề
\(6x^4+25x^3+12x-25x^2+6=0\)
\(\Leftrightarrow6x^4+12x^3+13x^3+26x^2-14x^2-28x+3x+6=0\)
\(\Leftrightarrow6x^3\left(x+2\right)+13x^2\left(x+2\right)-14x\left(x+2\right)+3\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(6x^3+13x^2-14x+3\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+3\right)\left(2x-1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=-3\\x=\dfrac{1}{2}\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy........
K
28 tháng 2 2018
Bài 1 : Giải phương trình
a) (x + 3)4 + (x + 5)4 = 16
Đặt : x + 3 = t
=> x + 5 = x + 3 + 2 = t + 2
Thay x + 3 = t và x + 5 = t + 2 vào phương trình, ta có :
t4 + (t + 2)4 = 16
<=> 2t4 + 8t3 + 24t2 + 32t + 16 = 16
<=> 2(t4 + 4t3 + 12t2 + 16t) = 0
<=> t4 + 4t3 + 12t2 + 16t = 0
<=> (t + 2) . t . (t2 + 2y + 4) = 0
TH1 : t = 0
TH2 : t + 2 = 0 <=> t = -2
TH3 : t2 + 2y + 4 = 0 (vô nghiệm => loại)
Nên t = 0 hoặc t = -2
hay x + 3 = -2 hoặc x + 3 = 0
<=> x = -5 hoặc x = -3
\(S=\left\{-5;-3\right\}\)
b) 6x4 + 25x3 + 12x2 - 25x + 6 = 0
<=> 6x4 + 12x3 + 13x3 + 26x2 - 14x2 - 28x + 3x + 6 = 0
<=> 6x3 (x + 2) + 13x2 (x + 2) - 14x (x + 2) + 3(x + 2) = 0
<=> (x + 2)(6x3 + 13x2 - 14x + 3) = 0
<=> (x + 2)(6x3 + 18x2 - 5x2 - 15x + x + 3) = 0
\(\Leftrightarrow\left(x+2\right)[6x^2\left(x+3\right)-5x\left(x+3\right)+\left(x+3\right)]=0\)
<=> (x + 2)(x + 3) (6x2 - 5x + 1) = 0
<=> (x + 2)(x + 3)(2x - 1)(3x - 1) = 0
TH1 : x + 2 = 0 <=> x = -2
TH2 : x + 3 = 0 <=> x = -3
TH3 : 2x - 1 = 0 <=> 2x = 1 <=> x = \(\dfrac{1}{2}\)
TH4 : 3x - 1 = 0 <=> 3x = 1 <=> 3x = \(\dfrac{1}{3}\)
\(S=\left\{-2;-3;\dfrac{1}{2};\dfrac{1}{3}\right\}\)
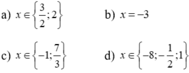
\(\Leftrightarrow21x-7x^2-12x^2+60x=0\Leftrightarrow-19x^2+81x=0\)
\(\Leftrightarrow x\left(-19x+81\right)=0\Leftrightarrow x=0;x=\dfrac{81}{19}\)