Bài 1: Thanh AB dài 160 cm, ở đầu A người ta treo một vật có khối lượng
m1 = 9kg điểm tựa O nằm cách A một đoạn 40cm.
a/ Hỏi phải treo vào đầu B một vật m2 có khối lượng bao nhiêu để
thanh cân bằng?
b/ Vật m2 giữ nguyên không đổi, bây giờ người ta di chuyển điểm tựa
O về phía đầu B và cách B một đoạn 60cm. Hỏi vật m1 ở đầu A phải thay đổi
như thế nào? Thêm hay bớt bao nhiêu?
Bài 2: Người ta dùng một thanh AB có chiều dài 120cm, ở đầu A treo vật m1 = 6kg, ở đầu B người ta treo vật m2 có khối lượng 4kg.
a/ Xác định vị trí điểm tựa O để thanh cân bằng.
b/ Giữa nguyên vật m2 và tăng khối lượng m1 lên 2kg. Để thanh AB tiếp tục cận bằng, thì điểm tựa O phải dịch chuyển như thế nào? Với một đoạn bằng bao nhiêu?

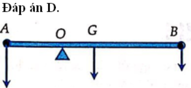
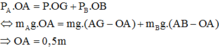
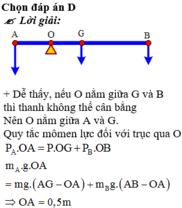
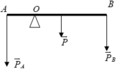

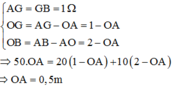
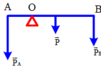
Bài 1.
a)\(OA=40cm\Rightarrow OB=160-40=120cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1\cdot l_1=F_2\cdot l_2\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{l_2}{l_1}=\dfrac{OB}{OA}=\dfrac{120}{40}=3\)
\(\Rightarrow F_2=\dfrac{F_1}{3}=\dfrac{P_1}{3}=\dfrac{10m_1}{3}=\dfrac{10\cdot9}{3}=30N\)
\(\Rightarrow m_2=\dfrac{P_2}{10}=\dfrac{F_2}{10}=\dfrac{30}{10}=3kg\)
b)Vật \(m_2\) giữ nguyên không đổi. \(\Rightarrow F_2=P_2=30N\)
\(OB'=60cm\Rightarrow OA'=160-60=100cm\)
Theo hệ cân bằng của đòn bẩy:
\(F_1'\cdot l_1'=F_2\cdot l_2'\)
\(\Rightarrow F_1'=\dfrac{F_2\cdot l_2'}{l_1'}=\dfrac{30\cdot60}{100}=18N\) \(\Rightarrow m_1'=1,8kg\)
Mà \(m_1=9kg\)
\(\Rightarrow\) Phải giảm vật đi một lượng là:
\(\Delta m=m_1-m_1'=9-1,8=7,2kg\)
Bài 2.
a)Áp dụng hệ cân bằng của đòn bẩy:
\(\dfrac{F_1}{F_2}=\dfrac{OA}{OB}=\dfrac{10m_1}{10m_2}=\dfrac{6}{4}=\dfrac{3}{2}\)
\(\Rightarrow2OA=3OB\left(1\right)\)
Mà \(OA+OB=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA=72cm\\OB=48cm\end{matrix}\right.\)
Vậy O nằm cách A và B lần lượt một đoạn là 72cm và 48cm.
b)Giữ nguyên vật 2 \(\Rightarrow F_2=P_2=10m_2=40N\)
Tăng khối lượng \(m_1\) lên 2kg thì \(F_1=P_1=10\cdot\left(2+6\right)=80N\)
Để thanh AB nằm cân bằng:
\(F_1\cdot OA'=F_2\cdot OB'\)
\(\Rightarrow\dfrac{F_1}{F_2}=\dfrac{OB'}{OA'}=\dfrac{80}{40}=2\)
\(\Rightarrow OB'=2OA'\left(1\right)\)
Mà \(OA'+OB'=120\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OA'=40cm\\OB'=80cm\end{matrix}\right.\)
Vậy O nằm trên AB cách A và B lần lượt là 40cm và 80 cm.