Cho đường tròn tâm O, bán kính OA bằng 10dm. Tính độ dài đường kính AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


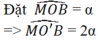 (góc nội tiếp và góc ở tâ của đường tròn (O'))
(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
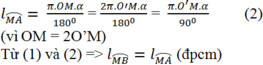


Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
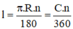

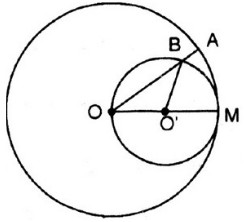
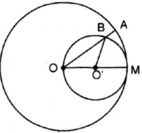
Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
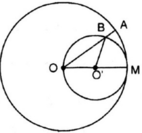
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

Đặt ˆMOB=αMOB^=α
⇒ˆMO′B=2α⇒MO′B^=2α (góc nội tiếp và góc ở tâm của đường tròn (O’))
Độ dài cung MB là:
lcungMB=π.O′M.2α1800=π.O′M.α900(1)lcungMB=π.O′M.2α1800=π.O′M.α900(1)
Độ dại cung MA là:
lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)lcungMA=π.OM.α1800=2π.O′M.α1800=πO′M.α900(2)
(Vì OM = 2O’M)
Từ (1) và (2) ⇒ sđcung MA = sđcung MB

b.
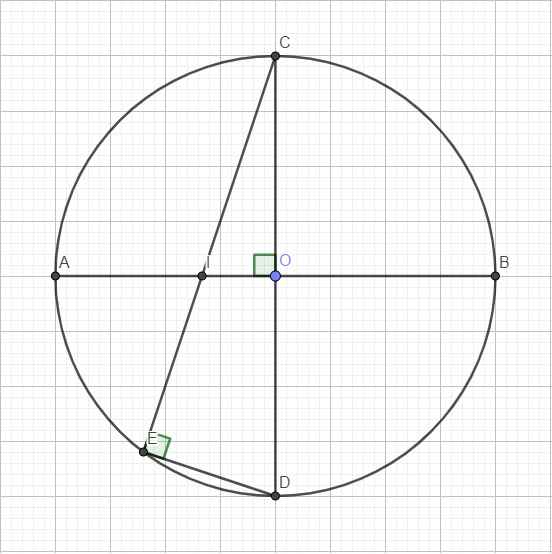
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
AB = 20dm
AB là: \(10\times2=20\left(dm\right)\)