Giúp tớ bài 3 đề 2 :3 camon 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\) + \(\dfrac{1}{3}\) = \(\dfrac{y}{5}\) và \(x\) + y = 15
\(x\) + y = 15 ⇒ \(x\) = 15 - y Thay vào \(x\) + \(\dfrac{1}{3}\) = \(\dfrac{y}{5}\) ta có:
15 - y + \(\dfrac{1}{3}\) = \(\dfrac{y}{5}\)
\(\dfrac{y}{5}\) + y = 15 + \(\dfrac{1}{3}\)
\(\dfrac{6y}{5}\) = \(\dfrac{46}{3}\)
y = \(\dfrac{46}{3}\) : \(\dfrac{6}{5}\)
y = \(\dfrac{115}{9}\)
thay y = \(\dfrac{115}{9}\) vào \(x\) = 15 - \(\dfrac{115}{9}\) ta có \(x\) = 15 - \(\dfrac{115}{9}\) ⇒ \(x\) = \(\dfrac{20}{9}\)
Vậy (\(x\); y) = (\(\dfrac{20}{9}\); \(\dfrac{115}{9}\))
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
(x + 1)/3 = y/5 = (x + 1 + y)/(3 + 5) = (15 + 1)/8 = 2
*) (x + 1)/3 = 8
x + 1 = 8.3
x + 1 = 24
x = 24 - 1
x = 23
*) y/5 = 8
y = 8.5
y = 40
Vậy x = 23; y = 40

\(a^2+b^2+c^2\ge2\left(a+b+c\right)-3\)
\(\Leftrightarrow a^2+b^2+c^2\ge2a+2b+2c-3\)
\(\Leftrightarrow a^2+b^2+c^2-2a-2b-2c+3\ge0\)
\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)\ge0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\) (luôn đúng)
Vậy \(a^2+b^2+c^2\ge2\left(a+b+c\right)-3\)

a) (3x - 1)³ + 17 = 710 : 5
(3x - 1)³ + 17 = 142
(3x - 1)³ = 142 - 17
(3x - 1)³ = 125
(3x - 1)³ = 5³
3x - 1 = 5
3x = 5 + 1
3x = 6
x = 6 : 3
x = 2

\(\frac{2a+3}{6}=-\frac{1}{b+5}\)
\(\left(2a+3\right)\left(b+5\right)=-6\)
a và b nguyên nên 2a+3 và b+5 là ước của -6
| 2a+3 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| b+5 | -6 | 6 | -3 | 3 | -2 | 2 | -1 | 1 |
| a | -1 | -2 | -0,5 | -2,5 | 0 | -3 | 1,5 | -4,5 |
| b | -11 | 1 | -8 | -2 | -7 | -3 | -6 | -4 |
Vậy bài toán có 4 đáp số là 4 cặp số:
a=-1 và b=-11
a=-2 và b=1
a=0 và b=-7
a=b=-3

c.
\(\left\{\begin{matrix} 9x-6y=4\\ 15x-10y=7\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=\frac{6y+4}{9}\\ 15x-10y=7\end{matrix}\right.\)
\(\Rightarrow 15.\frac{6y+4}{9}-10y=7\)
\(\Leftrightarrow \frac{5}{3}(6y+4)-10y=7\Leftrightarrow \frac{20}{3}=7\) (vô lý)
Do đó hpt vô nghiệm.
d.
\(\left\{\begin{matrix} 4x+5y=3\\ x-3y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4x+5y=3\\ x=3y+5\end{matrix}\right.\Rightarrow 4(3y+5)+5y=3\)
\(\Leftrightarrow 17y+20=3\Leftrightarrow 17y=-17\Leftrightarrow y=-1\)
\(x=3y+5=-3+5=2\)
Vậy HPT có nghiệm $(x,y)=(2,-1)$
Các câu còn lại bạn làm theo pp tương tự.
1.
HPT \(\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ 3x-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x-y=4\\ y=3x-5\end{matrix}\right.\)
\(\Rightarrow 5x-(3x-5)=4\Leftrightarrow 2x+5=4\Leftrightarrow 2x=-1\Leftrightarrow x=\frac{-1}{2}\)
\(y=3x-5=\frac{-3}{2}-5=\frac{-13}{2}\)
Vậy HPT có nghiệm $(x,y)=(\frac{-1}{2}, \frac{-13}{2})$



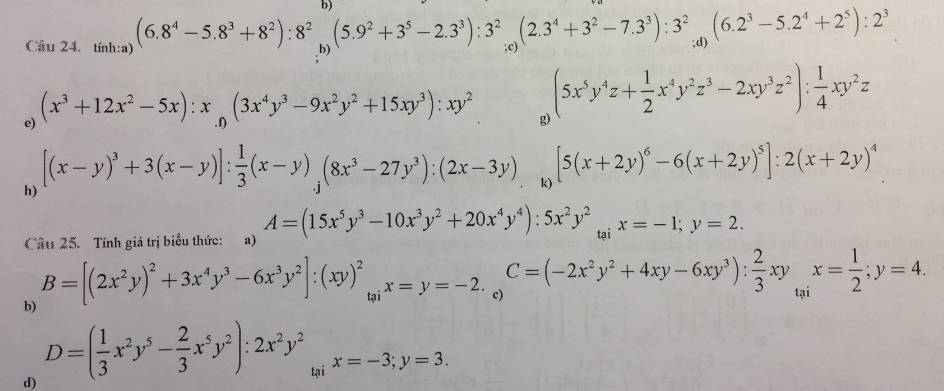
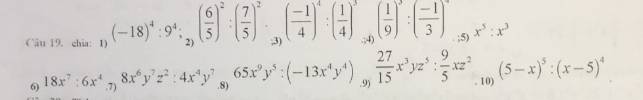 tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
Bài 1 :
Ta có : \(AC^2=BC^2+AB^2\Rightarrow625=225+400\left(luondung\right)\)
Vậy tam giác ABC vuông tại B