cho tam giác vuông ABC (A =90 độ). vẽ hình viết giả thiết và kết luận
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2023
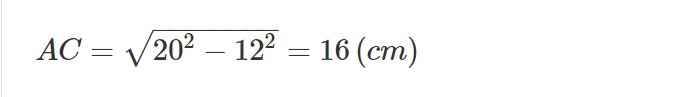
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm
28 tháng 2 2023
\(AC=\sqrt{20^2-12^2}=16\left(cm\right)\)
Xét ΔACB có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=20/7
=>DB=60/7cm; DC=80/7cm
2 tháng 1
Để tìm độ dài DA và DE, ta cần làm theo các bước sau:
1. Vẽ tam giác ABC, biết rằng góc A bằng 90 độ.
2. Trên cạnh BC, lấy điểm E sao cho BE = BA.
3. Vẽ tia phân giác của góc B, cắt AC tại điểm D.
4. Để tính độ dài DA và DE, ta có thể sử dụng định lí phép đổi vị trí.
Định lí phép đổi vị trí nói rằng trong tam giác vuông, nếu ta hoán đổi vị trí của các cạnh góc vuông và cạnh đối diện, thì độ dài 2 cạnh vuông góc với nhau sẽ không thay đổi.
Vì vậy, ta có: BD = BA (vì BD là cạnh đối diện góc vuông A),
và AD = AC (vì AD là cạnh vuông góc với BD).
5. Tiếp theo, để tính số đo góc BED, ta có thể sử dụng quy tắc cộng góc trong tam giác.
Ta biết rằng góc BED được tạo bởi tia BD và tia DE. Vì vậy, ta có:
BED = BDE + EDB.
Vì góc A là góc vuông, nên góc BAC + góc ABC + góc BCA = 180 độ (quy tắc tổng góc trong tam giác).
Vì góc ABC là góc vuông, nên góc BCA = 180 - góc BAC.
Vì vậy, góc EDB = góc ABC - góc BCA = 90 - (180 - góc BAC) = góc BAC - 90.
Do đó, góc BED = BDE + EDB = góc BAC + (góc BAC - 90) = 2góc BAC - 90.
Tóm lại, ta đã tìm được độ dài DA và DE là DA = AC và DE = BC, cũng như tính được số đo góc BED là 2góc BAC - 90.
H
22 tháng 4 2022
a, Xét △ABC và △DCE có
AC = CD
C^ đối đỉnh
BC = CE
=> △ABC = △DCE
b, VÌ △ABC = △DCE nên góc BAC = góc CDE
=> CDE = 90 độ
c, Vì BE = BC + CE = 20
Mà BC = CE = \(\dfrac{BC}{2}\) = \(\dfrac{20}{2}\) = 10
Vì AD = AC + CD = 16
Mà AC = CD = \(\dfrac{AD}{2}\) = \(\dfrac{16}{2}\) = 8
Áp dụng định lý Pytago
ta có : \(BC^2=AB^2+AC^2\)
\(10^2=AB^2+8^2\)
\(100=AB^2+64\)
\(AB^2=100-64=36\)
Vậy \(AB=6^2\)
Mong bạn tick cho mik :))
28 tháng 2 2023
Hình bạn tự vẽ nha
| GT | ΔACB vuông tại A, BD là phân giác, AB/CB=3/5; AC=16cm |
| KL | a: AB=?; BC=? b: AD=?; CD=? |
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm
BF
28 tháng 2 2023
Với `(AB)/(BC) = 3/5`
`=> (AB)/3 = (BC)/5`
Đặt `(AB)/3 = (BC)/5 = k (k > 0)`
`=> AB = 3k; BC = 5k`
Áp dụng định lý pitago vào tam giác `ABC` vuông tại `A`
`=> AB^2 + AC^2 = BC^2`
`=> (3k)^2 + 16^2 = (5k)^2`
`=> 9k^2 + 256 = 25k^2`
`=> 16k^2 = 256`
`=> k^2 = 16`
`=> k^2 = 4^2`
`=> k = 4 (`Vì `k > 0)`
Khi đó: `AB = 3k = 4 . 3 = 12 (cm)`
`BC = 5k = 5 . 4 = 20 (cm)`
b) Tam giác `ABC` có BD là tia phân giác của tam giác `ABC`. Áp dụng tính chất đường phân giác trong tam giác
`=> (AD)/(AB) = (DC)/(BC) `
`=> (AD)/12 = (DC)/20`
Áp dụng tính chất dãy tỉ số bằng nhau
`=> (AD)/12 = (DC)/20 = (AD + DC)/(12 + 20) = 16/32 = 1/2`
`=> AD = 1/2 xx 12 = 6 (cm) ; DC = 1/2 xx 20 = 10 (cm)`
28 tháng 2 2023
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm
KV
16 tháng 3 2023
GT ∆ABC cân tại A, AH BC
KL AHB = AHC
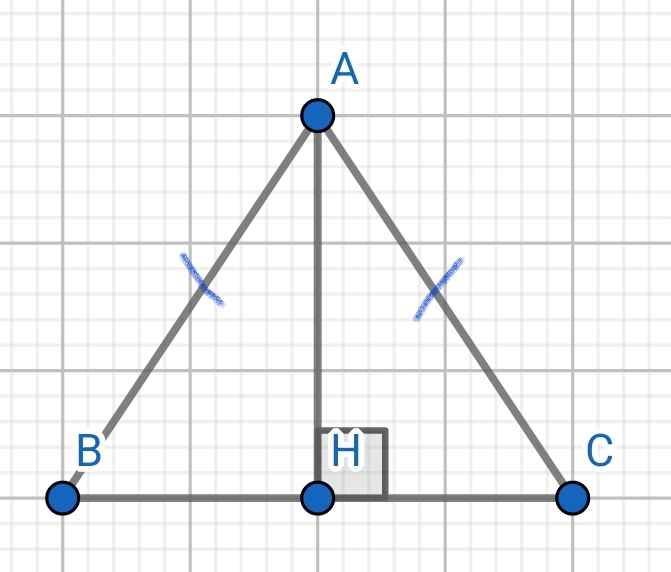
Xét hai tam giác vuông: ∆AHB và ∆AHC có:
AH chung
AB = AC (∆ABC cân tại A)
⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)
16 tháng 3 2023
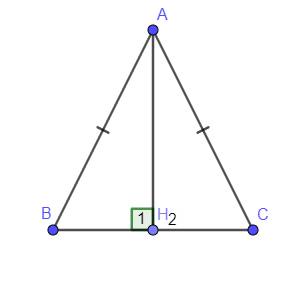
Có `AH⊥BC(GT)=>hat(H_1)=hat(H_2)(=90^0`
`Delta ABC` cân tại `A=>AB=AC`
Xét `Delta AHB` và `Delta AHC` có :
`{:(hat(H_1)=hat(H_2)(=90^0)),(AB=AC(cmt)),(AH-chung):}}`
`=>Delta AHB=Delta AHC(ch-cgv)(đpcm)`
28 tháng 2 2023
a: AB/BC=3/5
=>AB/3=BC/5=k
=>AB=3k; BC=5k
BC^2=AB^2+AC^2
=>16k^2=16^2=256
=>k^2=16
=>k=4
=>AB=12cm; CB=20cm
b: BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=16/8=2
=>AD=6cm; CD=10cm
gỈA THIẾT | CHO TAM GIÁC VÔNG abc
kết luận | ?