Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) \(KC=\dfrac{1}{2}\times KB\Rightarrow KC=\dfrac{1}{3}\times BC\)
\(S_{AKC}=\dfrac{1}{3}\times S_{ABC}\) (chung đường cao hạ từ \(A\), \(KC=\dfrac{1}{3}\times BC\))
\(S_{AHK}=\dfrac{1}{4}\times S_{AKC}\) (chung đường cao hạ từ \(K\), \(AH=\dfrac{1}{4}\times AC\))
\(=\dfrac{1}{4}\times\dfrac{1}{3}\times S_{ABC}=\dfrac{1}{12}\times S_{ABC}\)
\(S_{HKC}=S_{AKC}-S_{AHK}=\dfrac{1}{3}\times S_{ABC}-\dfrac{1}{12}\times S_{ABC}=\dfrac{1}{4}\times S_{ABC}\)
b) \(S_{AHK}=\dfrac{1}{12}\times S_{ABC}\Leftrightarrow S_{ABC}=12\times S_{AHK}=12\times4,5=54\left(cm^2\right)\)
Theo đề ra, ta có:
\(DK=\dfrac{1}{3}BC\)
\(ME=\dfrac{1}{3}CA\)
\(HN=\dfrac{1}{3}AB\)
\(\Rightarrow S_{\Delta ADK}=\dfrac{1}{9}S_{\Delta ABC}=\dfrac{1}{9}\times270=30cm^2\)
Tương tự, ta có:
\(S_{\Delta AHN}=\dfrac{1}{9}S_{\Delta ABC}=\dfrac{1}{9}\times270=30cm^2\)
\(\Rightarrow S_{\Delta BME}=30cm^2\)
\(S_{DEMNKH}=S_{ABC}-3\times S_{AKD}=180cm^2\)
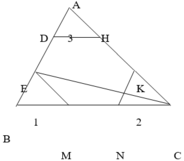
+ SABC – (S1 + S2 + S3) = SDEMNHK
- Nối C với E, ta tính được :
SCEB = 1/3 SCAB (Vì cùng chiều cao hạ từ C xuống AB, đáy BE = 1/3 BC).
Hay S1 = 1/9 SABC .
+ Tương tự ta tính :
S1 = S2 = S3 = 1/9 SABC và bằng 270 : 9 = 30 (cm2)
+ Từ đó ta tính được :
SDEMNKH = 180 (cm2)
Đáp số 180 cm2
Bạn tham khảo tại link này nhé
https://olm.vn/hoi-dap/detail/86879399868.html
Diện tích hình tam giác HCK bé hơn diện tích hình tam giác ABC.
Chúc bạn học tốt.
😁😁😁