X2-2(m-1)x+m2-4m+5=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 4 2023
Thay x=5 vào pt, ta được:
25-10(m+1)+m^2-4m+5=0
=>m^2-4m+30-10m-10=0
=>m^2-14m+20=0
=>\(m=7\pm\sqrt{29}\)
x1+x2=(2m+2)
=>x2+5=16+2 căn 29 hoặc x2+5=16-2 căn 29
=>x2=11+2căn 29 hoặc x2=11-2 căn 29
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)
22 tháng 1 2022
a: \(\Leftrightarrow\left(2m-2\right)^2-4\left(m^2-2\right)>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2+8>=0\)
=>-8m>=-12
hay m<=3/2
b: \(\Leftrightarrow\left(4m-4\right)^2-4\cdot\left(-2\right)\cdot\left(4m-6\right)>0\)
\(\Leftrightarrow16m^2-32m+16+32m-48>0\)
\(\Leftrightarrow16m^2>32\)
hay \(\left[{}\begin{matrix}m>\sqrt{2}\\m< -\sqrt{2}\end{matrix}\right.\)
22 tháng 1 2022
\(a,\Delta'=\left[-\left(m-1\right)\right]^2-1\left(m^2-2\right)\\ =m^2-2m+1-m^2+2\\ =-2m+3\)
Để pt có nghiệm thì \(\Delta'\ge0\) hay
\(\Leftrightarrow-2m+3\ge0\\ \Leftrightarrow m\le\dfrac{3}{2}\)
\(b,\Delta'=\left[-2\left(m-1\right)\right]^2-\left(-2\right)\left(4m-6\right)\\ =4\left(m^2-2m+1\right)+2\left(4m-6\right)\\ =4m^2-8m+4+8m-12\\ =4m^2-8\)
Để pt có 2 nghiệm phân biệt thì \(\Delta'>0\) hay
\(4m^2-8>0\\ \Leftrightarrow\left[{}\begin{matrix}x< -\sqrt{2}\\x>\sqrt{2}\end{matrix}\right.\)
DT
23 tháng 4 2022
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
28 tháng 1 2024
a: \(\text{Δ}=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(m^2-4m+5\right)\)
\(=4\left(m+1\right)^2-4\left(m^2-4m+5\right)\)
\(=4m^2+8m+4-4m^2+16m-20\)
=24m-16
Để phương trình có hai nghiệm thì Δ>=0
=>24m-16>=0
=>24m>=16
=>\(m>=\dfrac{2}{3}\)
b: Bạn xem lại đề nha bạn
CM
15 tháng 3 2018
2 x 2 – (4m + 3)x + 2 m 2 – 1 = 0 (2)
Phương trình (2) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có: ∆ = - 4 m + 3 2 – 4.2(2 m 2 – 1)
= 16 m 2 + 24m + 9 – 16 m 2 + 8 = 24m + 17
∆ ≥ 0 ⇔ 24m + 17 ≥ 0 ⇔ m ≥ -17/24
Vậy khi m ≥ -17/24 thì phương trình đã cho có nghiệm.
Giải phương trình (2) theo m:
CM
3 tháng 7 2019
Chọn A
Ta có y ' = 3 x 2 + 4 ( m - 1 ) x + m 2 - 4 m + 1 . Hàm số có hai cực trị
=> y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=> 4 ( m - 1 ) 2 - 3 ( m 2 - 4 m + 1 ) > 0
<=> m 2 + 4 m + 1 > 0
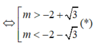
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt x 1 , x 2 ta có
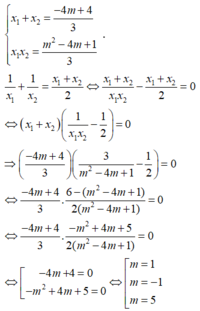
Đối chiếu điều kiện (*) có m = 5 hoặc m = 1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
\(\Delta'=\left(m+1\right)^2-\left(m^2-4m+5\right)=6m-4\)
Phương trình có 2 nghiệm pb khi:
\(6m-4>0\Rightarrow m>\dfrac{2}{3}\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2-4m+5\end{matrix}\right.\)
Do \(m>\dfrac{2}{3}\Rightarrow2\left(m+1\right)>2\left(\dfrac{2}{3}+1\right)>0\)
Đồng thời \(m^2-4m+5=\left(m-2\right)^2+1>0;\forall m\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Rightarrow\) cả hai nghiệm của pt đều dương
CM
4 tháng 4 2017
Đáp án B.
Gọi điểm cố định là A ( x 0 ; y 0 )
⇒ y 0 = x 0 3 − 3 ( m + 1 ) x 0 2 + 2 ( m 2 + 4 m + 1 ) x 0 − 4 m ( m + 1 ) ∀ m
⇔ 2 ( x 0 − 2 ) m 2 − ( 3 x 0 2 − 8 x 0 + 4 ) m + x 0 3 − 3 x o 2 + 2 x 0 − y 0 = 0 ∀ m
⇔ x 0 − 2 = 0 3 x 0 2 − 8 x 0 + 4 = 0 x 0 3 − 3 x 0 2 + 2 x 0 − y 0 = 0 ⇔ x 0 = 2 y 0 = 0 ⇒ A ( 2 ; 0 )
=>Có một điểm cố định
xin lỗi mih lớp 7 thui ak