Cho ΔABC nhọn, đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Gọi K là giao điểm của MN và BC.Chứng minh KH^2=KB.KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BM // NH. ta có : \(\frac{KB}{KH}=\frac{KM}{KN}\)
MH // NC . ta có : \(\frac{KM}{KN}=\frac{KH}{KC}\)
\(\Rightarrow\frac{KB}{KH}=\frac{KH}{KC}\)
\(\Rightarrow KB.KB=KH^2\)

a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
Do đó: AMHN là hình chữ nhật
Suy ra: MN=AH
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC=AH^2\)

a: Xét ΔABC có
M là trung điểm của BA
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
=>MN=BE và MN//BE
=>BMNE là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM
=>M nằm trên đường trung trực của AH(1)
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến
nên HN=AC/2=AN
=>N nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra MN là đường trung trực của AH
Xét ΔABC có
M là trung điểm của AB
E là trung điểm của BC
Do đó: ME là đường trung bình
=>ME=AC/2
mà HN=AC/2
nên ME=HN
Xét tứ giác MNEH có MN//EH
nên MNEH là hình thang
mà ME=NH
nên MNEH là hình thang cân

a: Xét tứ giác BMDH có
gócc BMD+góc BHD=180 độ
=>BMDH là tứ giác nội tiếp
b: góc AMN+góc OAM
=góc ADN+(180 độ-góc AOB)/2
=90 độ-góc HAC+90 độ-góc AOB/2
=180 độ-(90 độ-góc ACB)-góc ACB
=90 độ
=>MN vuông góc AO
=>MN//tiếp tuyến tại A của (O)

a: Xét ΔABC có
M,N lần lượt là trung điểm của AB và AC
nên MN là đường trung bình
=>MN//BC và MN=BC/2
=>MN//BE và MN=BE
=>BMNE là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM(1)
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến
nên HN=AN(2)
Từ (1)và (2) suy ra AH là đường trung trực của MN
Xét ΔABC có
E,M lần lượt là trung điểm của CB và BA
nên ME là đường trung bình
=>ME=CA/2=NH
Xét tứ giác MNEH có MN//EH
nên MNEH là hình thang
mà ME=NH
nên MNEH là hình thang cân

a: Xét ΔAHC vuông tại H có sin C=AH/AC
=>AH/8=sin30=1/2
=>AH=4cm
HC=căn AC^2-AH^2=4*căn 3(cm)
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF và ΔACB có
AE/AC=AF/AB
góc A chung
=>ΔAEF đồng dạng với ΔACB
=>góc AEF=góc ACB

a: Xét tứ giác ADHE có
\(\widehat{DAE}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE
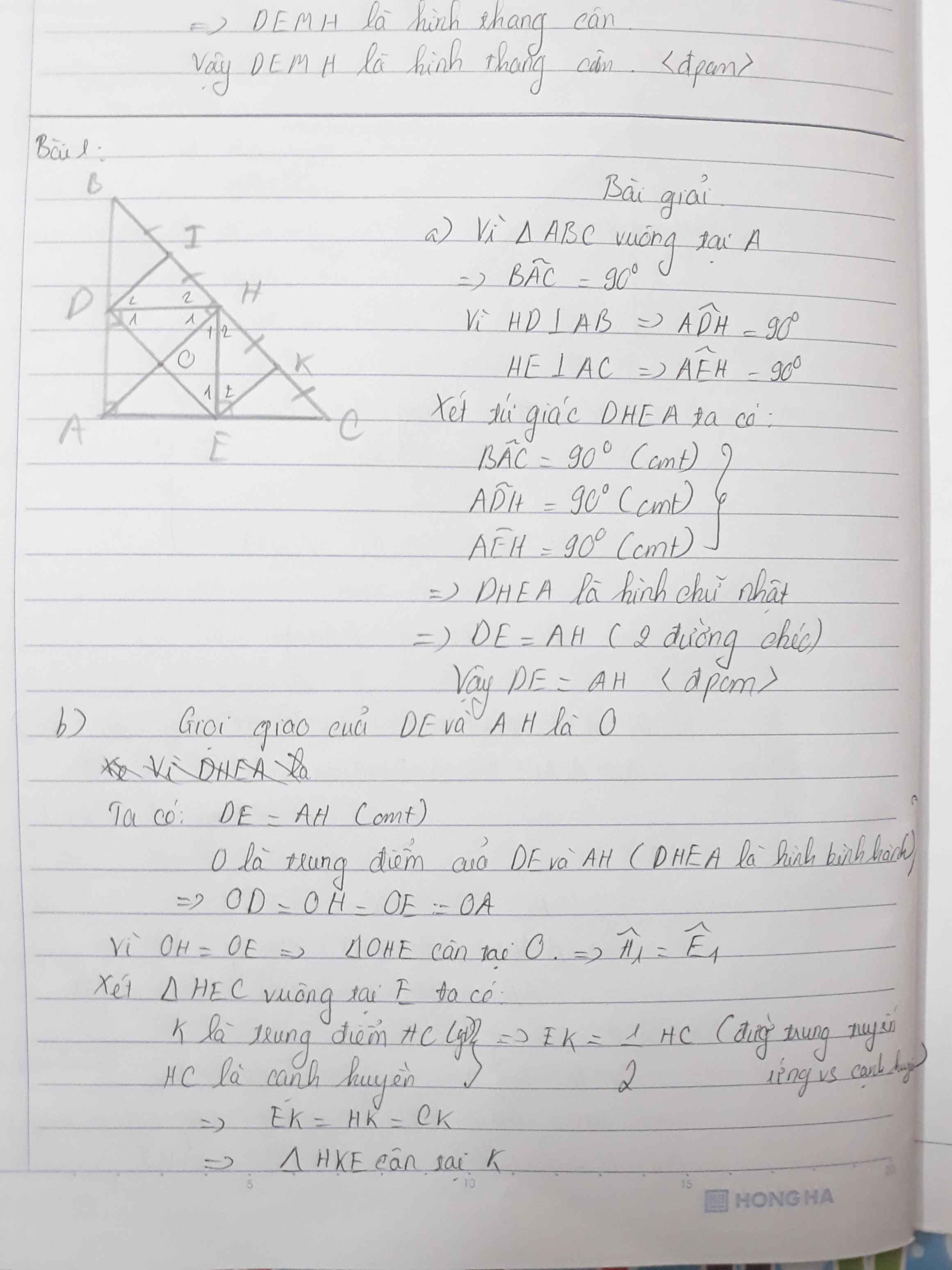
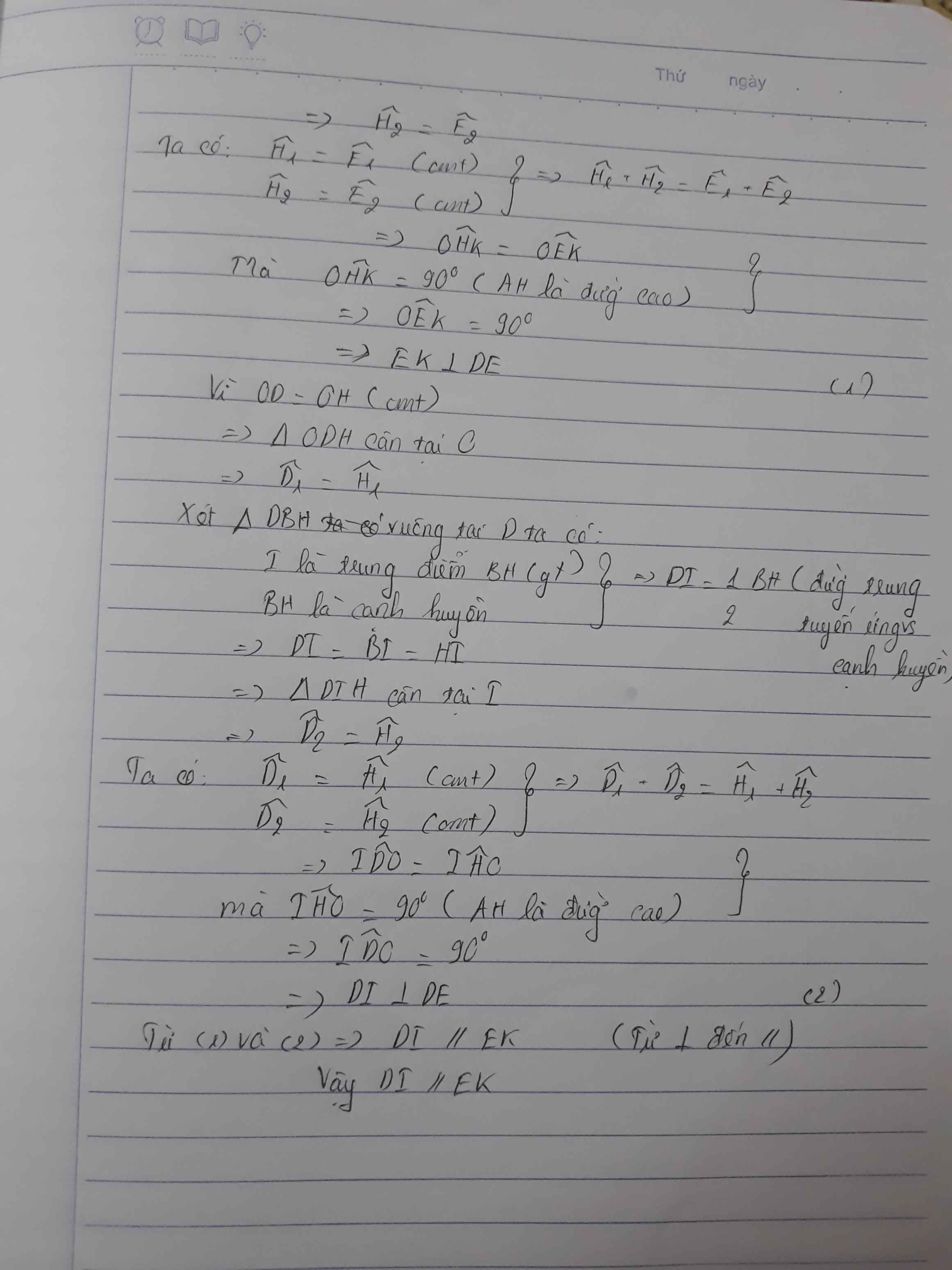
Gọi I là trung điểm AH
M và N đều nhìn AH dưới 1 góc vuông \(\Rightarrow\) tứ giác AMHN nội tiếp đường tròn (I) đường kính AH
Mặt khác \(IH\perp KH\Rightarrow KH\) là tiếp tuyến của (I)
Theo tính chất phương tích: \(KH^2=KM.KN\)
Lại có: \(\widehat{AHN}=\widehat{ACB}\) (cùng phụ \(\widehat{HAN}\))
\(\widehat{AHN}=\widehat{AMN}\) (cùng chắn cung AN của đường tròn (I))
\(\widehat{AMN}=\widehat{KMB}\) (đối đỉnh)
\(\Rightarrow\widehat{KMB}=\widehat{ACB}\)
Xét hai tam giác KMB và KCN có:
\(\left\{{}\begin{matrix}\widehat{BKM}\text{ chung}\\\widehat{KMB}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta KMB\sim\Delta KCN\left(g.g\right)\)
\(\Rightarrow\dfrac{KB}{KN}=\dfrac{KM}{KC}\Rightarrow KM.KN=KB.KC\)
\(\Rightarrow KH^2=KB.KC\)