Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Xét △AMD và △AHB có: \(\widehat{AMD}=\widehat{AHB}\left(=90^0\right)\), \(\widehat{BAH}\) là góc chung.
\(\Rightarrow\Delta AMD\sim\Delta AHB\left(g-g\right)\)
\(\Rightarrow\dfrac{AM}{AH}=\dfrac{AD}{AB}\Rightarrow AM.AB=AD.AH\left(1\right)\)
- Xét △AND và △AHC có: \(\widehat{AND}=\widehat{AHC}=90^0\), \(\widehat{CAH}\) là góc chung.
\(\Rightarrow\Delta AND\sim\Delta AHC\left(g-g\right)\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AN}{AH}\Rightarrow AD.AH=AN.AC\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AM.AB=AN.AC\Rightarrow\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét △AMN và △ACB có: \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)(cmt), \(\widehat{BAC}\) là góc chung.
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(c-g-c\right)\)
\(\Rightarrow\widehat{AMN}=\widehat{ACB}\)
Ta có \(OA=OB\) nên △OAB cân tại O.
\(\Rightarrow\widehat{OAB}=\dfrac{180^0-\widehat{AOB}}{2}\)
Xét (O): \(\widehat{AOB}=2\widehat{ACB}\left(=sđ\stackrel\frown{AB}\right)\)
\(\Rightarrow\widehat{OAB}=\dfrac{180^0-2\widehat{ACB}}{2}=90^0-\widehat{ACB}\)
\(\Rightarrow\widehat{OAB}+\widehat{AMN}=90^0\) nên MN vuông góc với OA.
=>MN song song với tiếp tuyến tại A của (O) (vì OA là bán kính của (O) ).

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

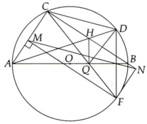
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!
a: Xét tứ giác BMDH có
gócc BMD+góc BHD=180 độ
=>BMDH là tứ giác nội tiếp
b: góc AMN+góc OAM
=góc ADN+(180 độ-góc AOB)/2
=90 độ-góc HAC+90 độ-góc AOB/2
=180 độ-(90 độ-góc ACB)-góc ACB
=90 độ
=>MN vuông góc AO
=>MN//tiếp tuyến tại A của (O)