 Ai giải hộ em ạ
Ai giải hộ em ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: =-3/7-5/9+3/7=-5/9
b: \(=\dfrac{5}{7}\left(\dfrac{2}{11}+\dfrac{3}{11}-\dfrac{16}{11}\right)=\dfrac{-5}{7}\)
c: \(=\dfrac{5}{4}-\dfrac{1}{4}\cdot\dfrac{-16}{3}+1=\dfrac{9}{4}+\dfrac{4}{3}=\dfrac{43}{12}\)



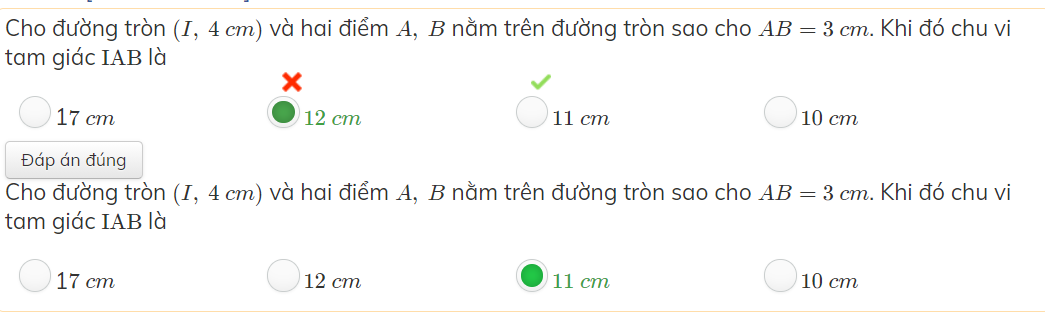
A, B thuộc đường tròn nên \(IA=IB=R=4\left(cm\right)\)
Chu vi tam giác: \(IA+IB+AB=4+4+3=11\left(cm\right)\)

a: \(\text{Δ}=1-4m\)
Để phương trình vô nghiệm thì -4m+1<0
=>m>1/4
Để phương trình có nghiệm kép thì -4m+1=0
hay m=1/4
Để phương trình có vô số nghiệm thì -4m+1>0
hay m<1/4
b: \(\text{Δ}=9-4\cdot1\cdot\left(-m\right)=4m+9\)
Để phương trình vô nghiệm thì 4m+9<0
hay m<-9/4
Để phương trình có nghiệm kép thì 4m+9=0
hay m=-9/4
Để phương trình có 2 nghiệm phân biệt thì 4m+9>0
hay m>-9/4
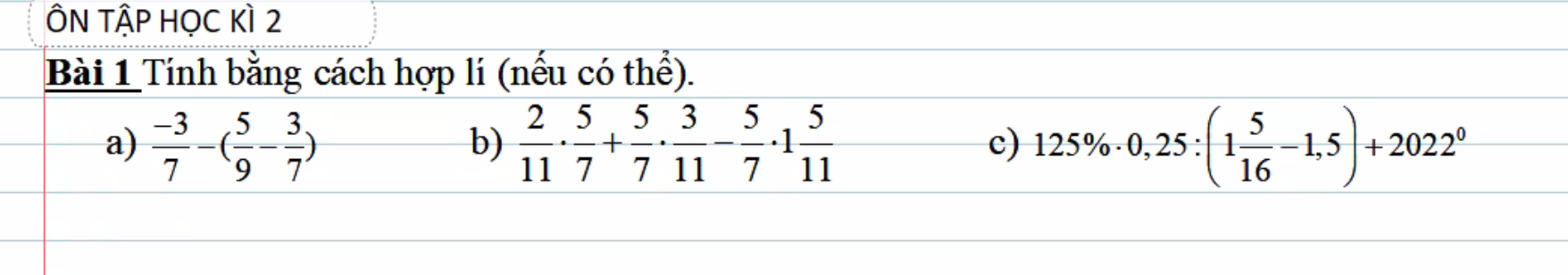





1.3.1
Cây Thân cao, muộn lai vs cây thân thấp, sớm -> F1 thu đc 100% thân cao, sớm
=> Cao (A) trội hoàn toàn so vs thấp (a)
Sớm (B) trội hoàn toàn so với muộn (b)
Xét F2 : có : \(\dfrac{cao, sớm}{tổng số cây}\) = \(\dfrac{1800}{3200}=\dfrac{9}{16}\)
Số tổ hợp 16 = 4 x 4 -> Mỗi bên F1 đều sinh ra 4 loại giao tử với tỉ lệ ngang nhau (trong đó có giao tử AB)
-> Phép lai tuân theo quy luật phân ly độc lập
-> F1 có KG : AaBb
( * ở tỉ lệ 9/16 hay 1/16 đều chứng mih đc PLĐL và KG bố mẹ dị hợp)
-> P có KG : AAbb x aaBB (cao, muộn x thấp, sớm)
Sđlai :
Ptc : AAbb x aaBB
G : Ab aB
F1 : 100% AaBb (100% cao, sớm)
F1 x F1 : AaBb x AaBb
G : AB;Ab;aB;ab AB;Ab;aB;ab
F2 : KG : 1AABB : 2AABb : 2AaBB : 4AaBb : 1AAbb : 2Aabb : 1aaBB :
2aaBb : 1aabb
KH : 9 cao, sớm : 3 cao, muộn : 3 thấp, sớm : 1 thấp, muộn
1.3.2
Tỉ lệ KH F2 : \(\dfrac{9}{16}\) cao, sớm : \(\dfrac{3}{16}\) cao, muộn : \(\dfrac{3}{16}\) thấp, sớm : \(\dfrac{1}{16}\) thấp, muộn
Số cây có KH cao, sớm : \(\dfrac{9}{16}.3200=1800\left(cây\right)\)
Số cây có KH cao, sớm : \(\dfrac{3}{16}.3200=600\left(cây\right)\)
Số cây có KH cao, sớm : \(\dfrac{3}{16}.3200=600\left(cây\right)\)
Số cây có KH cao, sớm : \(\dfrac{1}{16}.3200=200\left(cây\right)\)