1+1=11 tại sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
13 tháng 4 2019
Vì 1 + 1 = 10 là hệ số nhị phân
11 + 1 = 100 là hệ số nhị phân
1 + 1 = 10(2)
11 + 1 = 100(2)
NK
3
VT
1
T
13 tháng 6 2020
sai đề bài ko bạn nhỉ.
theo mình thì 1+2+3+4+....+11+12 = 78 thì mới tính được
đặt A = 1+2+3+4+....+11+12
ta có A = 12+11+10+9+.....+2+1
suy ra 2A =[ 1+12 ] + [ 11+2 ] + [ 10+3 ] + [ 9+4 ] +.....+ [ 2+11 ] + [ 1+12 ]
2A= 13 + 13 + 13 + 13 +.....+ 13 + 13
2A = 13 * 12 [ vì A có 12 số hạng ] * là dấu nhân bạn nhé
2A =156
A = 156 ; 2 = 78 [ ; là dấu chia ]
nhớ kết bạn với mình
CHÚC BẠN HỌC TỐT
1 tháng 8 2023
Tham khảo!
- Trong sản xuất chè, người dân cắt ngắn bớt thân, cành chè vào tháng 11 đến tháng 1 hằng năm vì cắt ngắn bớt thân, cành chè nhằm loại bỏ ưu thế đỉnh, kích thích cây mọc chồi mới, sinh trưởng mạnh và ra hoa chậm, cho nhiều chồi mới nhằm tăng năng suất búp chè. Cắt ngắn bớt thân, cành chè còn giúp tập trung chất dinh dưỡng nuôi chồi mới, loại bỏ các cành giá yếu, sâu bệnh; giúp chồi mới sinh trưởng mạnh hơn.
B
Tìm tất cả các số nguyên dương k sao cho tồn tại số nguyên dương n thỏa mãn 2n+11 chia hết cho 2k-1.
1
DD
29 tháng 6 2023
Để tìm tất cả các số nguyên dương k thỏa mãn điều kiện đã cho, ta sẽ giải phương trình theo n.
2n + 11 chia hết cho 2k - 1 có nghĩa là tồn tại một số nguyên dương m sao cho:
2n + 11 = (2k - 1)m
Chuyển biểu thức trên về dạng phương trình tuyến tính:
2n - (2k - 1)m = -11
Ta nhận thấy rằng nếu ta chọn một số nguyên dương nào đó, ta có thể tìm được một số nguyên dương k tương ứng để phương trình trên có nghiệm. Do đó, ta chỉ cần tìm tất cả các số nguyên dương n thỏa mãn phương trình trên.
Để giải phương trình này, ta có thể sử dụng thuật toán Euclid mở rộng (Extended Euclidean Algorithm). Tuy nhiên, trong trường hợp này, ta có thể tìm được một số giá trị n và k thỏa mãn phương trình bằng cách thử từng giá trị của n và tính giá trị tương ứng của k.
Dưới đây là một số cặp giá trị n và k thỏa mãn phương trình đã cho:
(n, k) = (3, 2), (7, 3), (11, 4), (15, 5), (19, 6), …
Từ đó, ta có thể thấy rằng có vô số giá trị n và k thỏa mãn phương trình đã cho.
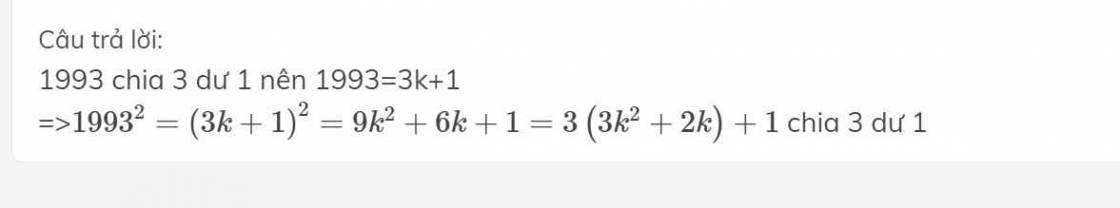
1+1=11
vì 1 thêm 1 bằng 11
hoặc tại ta tính sai
tại ngu tính sai