Mn giúp mik vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
TK
1
DT
Đỗ Thanh Hải
CTVVIP
6 tháng 9 2021
C
1 cooking
2 listening
3 reading
4 playing
5 cycling
1 People collect a lot of things such as stamps, milk bottle labels, comic books as well as car toys
2 She is 20 years old
3 She is a hairdresser
4 It is collecting candy shells
5 Her friends and relatives
B
1 F
2 F
3 F
4 F
5 T
NT
6 tháng 9 2021
c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
KK
6 tháng 9 2021
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)
NN
4
29 tháng 10 2021
Bài 5:
\(A=2A-A=2^2+2^3+...+2^{107}-2-2^2-...-2^{2016}=2^{107}-2\)
\(2\left(A+2\right)=2^{2x}\\ \Rightarrow2\left(2^{107}-2+2\right)=2^{2x}\\ \Rightarrow2^{108}=2^{2x}\\ \Rightarrow2x=108\\ \Rightarrow x=54\)
29 tháng 10 2021
Bài 3:
Gọi số học sinh lớp 7A, 7B lần lượt là a,b
Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{y}{9}\\y-x=5\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-1}=\dfrac{5}{1}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{9}=5\Rightarrow y=45\)
Vậy số học sinh lớp 7A, 7B lần lượt là 40, 45 học sinh
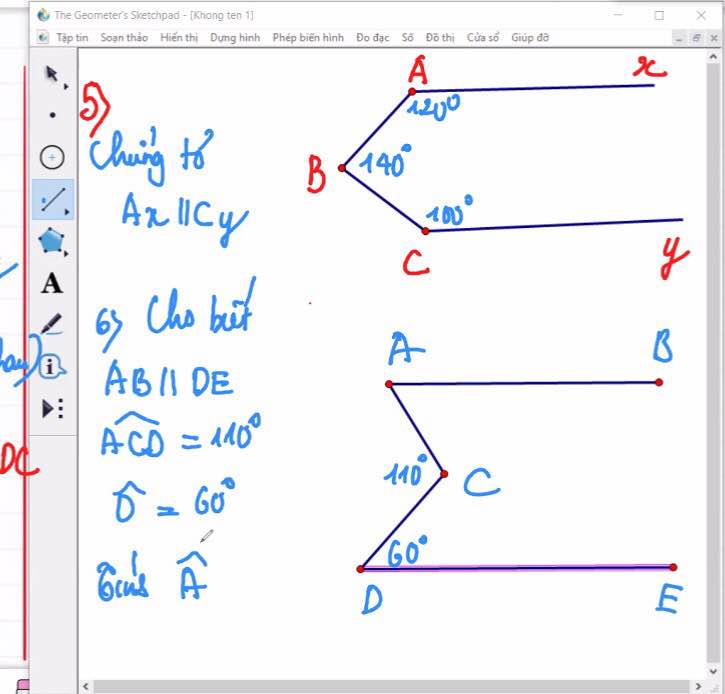
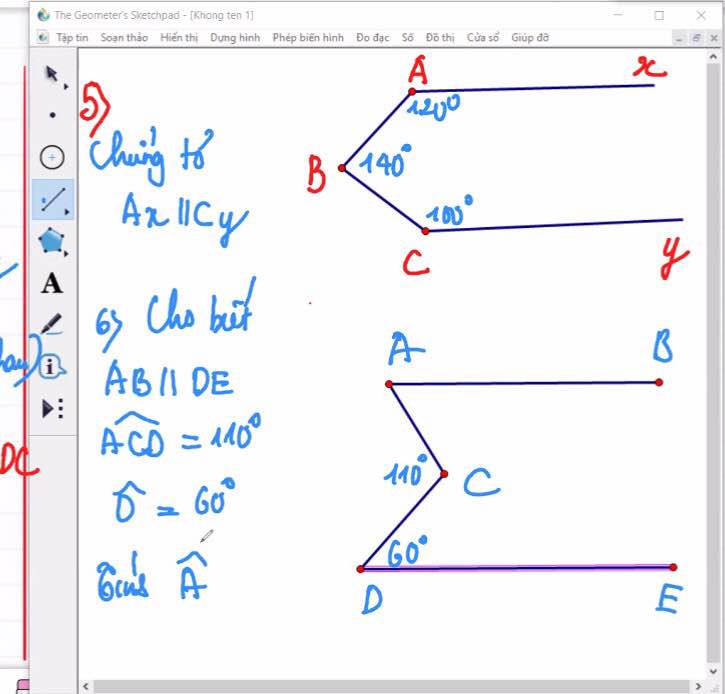
Câu 3:
a.
Biến đổi biểu thức A ta được:
\(A=\dfrac{x}{1-x}+\dfrac{5}{x}=\dfrac{x^2-5x+5}{x-x^2}\)
Ta có:
\(A-\left(5+2\sqrt{5}\right)=\dfrac{\left[\left(12+4\sqrt{5}\right)x-10-2\sqrt{5}\right]^2}{24+8\sqrt{5}}\ge0\)
Do đó:
\(A_{min}=5+2\sqrt{5}\) khi \(x=\dfrac{5-\sqrt{5}}{4}\)
b.
Từ giả ta có các nhận xét sau
\(\sqrt{2022}=\Sigma\sqrt{a^2+b^2}\ge\Sigma\dfrac{a+b}{\sqrt{2}}=\sqrt{2}\left(a+b+c\right)\)
\(\Rightarrow a+b+c\le\sqrt{1011}\)
\(\sqrt{2022}=\Sigma\sqrt{a^2+b^2}\le\sqrt{3\left[2\left(a^2+b^2+c^2\right)\right]}\)
\(\Rightarrow a^2+b^2+c^2\ge337\)
Do vai trò của a, b, c bình đẳng nên ta có thể giả sử:
\(a\le b\le c\)
\(\Rightarrow\left\{{}\begin{matrix}a^2\le b^2\le c^2\\\dfrac{1}{b+c}\le\dfrac{1}{c+a}\le\dfrac{1}{a+b}\end{matrix}\right.\)
Áp dụng bđt Chebyshev cho hai bộ số cùng chiều
\(\left(a^2,b^2,c^2\right)\) và \(\left(\dfrac{1}{b+c},\dfrac{1}{c+a},\dfrac{1}{a+b}\right)\) :
\(VT\ge\dfrac{1}{3}.\left(a^2+b^2+c^2\right)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge\dfrac{3\left(a^2+b^2+c^2\right)}{2\left(a+b+c\right)}\ge\dfrac{\sqrt{1011}}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{\sqrt{1011}}{3}\)