Cho tam giác ABC, phân giác AD. Vẽ đường tròn tâm O qua A và tiếp xúc với BC tại D cắt các cạnh AB và AC lần lượt tại E và F. Chứng minh rằng:
a) EF//BC
b) AB.BE= BD^2
c) tam giác ADF đồng dạng với tam giác ABD
d) AD^2= AC.AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

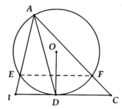
a, HS tự chứng minh
b, ∆ADE:∆ACD (g.g)
=> A D 2 = A E . A C
c, Tương tự: ∆ADF:∆ABD => A D 2 = A B . A F => ĐPCM

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại I
b: Ta có: \(\widehat{AMO}=\widehat{ANO}=\widehat{AIO}\)
=>A,M,I,O,N cùng thuộc đường tròn đường kính AO
Gọi I là trung điểm của AO
=>A,M,I,O,N cùng thuộc (I)
Xét (O) có
AM,AN là các tiếp tuyến
Do đó: OA là phân giác của góc MON
=>\(\widehat{MOA}=\widehat{NOA}\)
Xét (I) có
\(\widehat{MOA}\) là góc nội tiếp chắn cung MA
\(\widehat{NOA}\) là góc nội tiếp chắn cung NA
\(\widehat{MOA}=\widehat{NOA}\)
Do đó: \(sđ\stackrel\frown{MA}=sđ\stackrel\frown{NA}\)
Xét (I) có
\(\widehat{MIA}\) là góc nội tiếp chắn cung MA
\(\widehat{NIA}\) là góc nội tiếp chắn cung NA
\(sđ\stackrel\frown{MA}=sđ\stackrel\frown{NA}\left(cmt\right)\)
Do đó: \(\widehat{MIA}=\widehat{NIA}\)
=>IA là phân giác của góc MIN

Xét 2 tg AED và ADC có
^EAD=^DAC (đề bài) (1)
Ta có:
^AEF=^ADF (Góc nt cùng chắn cung AF)
^DEF= 1/2 số đo cung DF (góc nt)
^CDF=1/2 số đo cung DF (góc giới hạn bởi tiếp tuyến và dây cung)
=> ^AEF+^DEF=^AED=^ADF+^CDF=^ADC (2)
Từ (1) và (2) => tg AED và tg ADC đồng dạng
=> AE/AD=AD/AC => AD^2=AE.AC