Cho (O) đường kính AB, M là một điểm cố định trên tiếp tuyến tại A của (O). Vẽ tiếp tuyến MC và cát tuyến MHK (H nằm giữa M và K; tia MK nằm giữa hai tia MB, MO). Các đường thẳng BH, BK cắt đường thẳng MO tại E và F. a) Chứng minh rằng tứ giác AMCO, tứ giác MGKC và tứ giác MCHE nội tiếp b) Qua A kẻ đường thẳng song song với MK, cắt (O) tại I, CI cắt MK tại N. Chứng minh NH = NK c) OE = OF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

DT
Đỗ Tuệ Lâm
4 tháng 2 2022

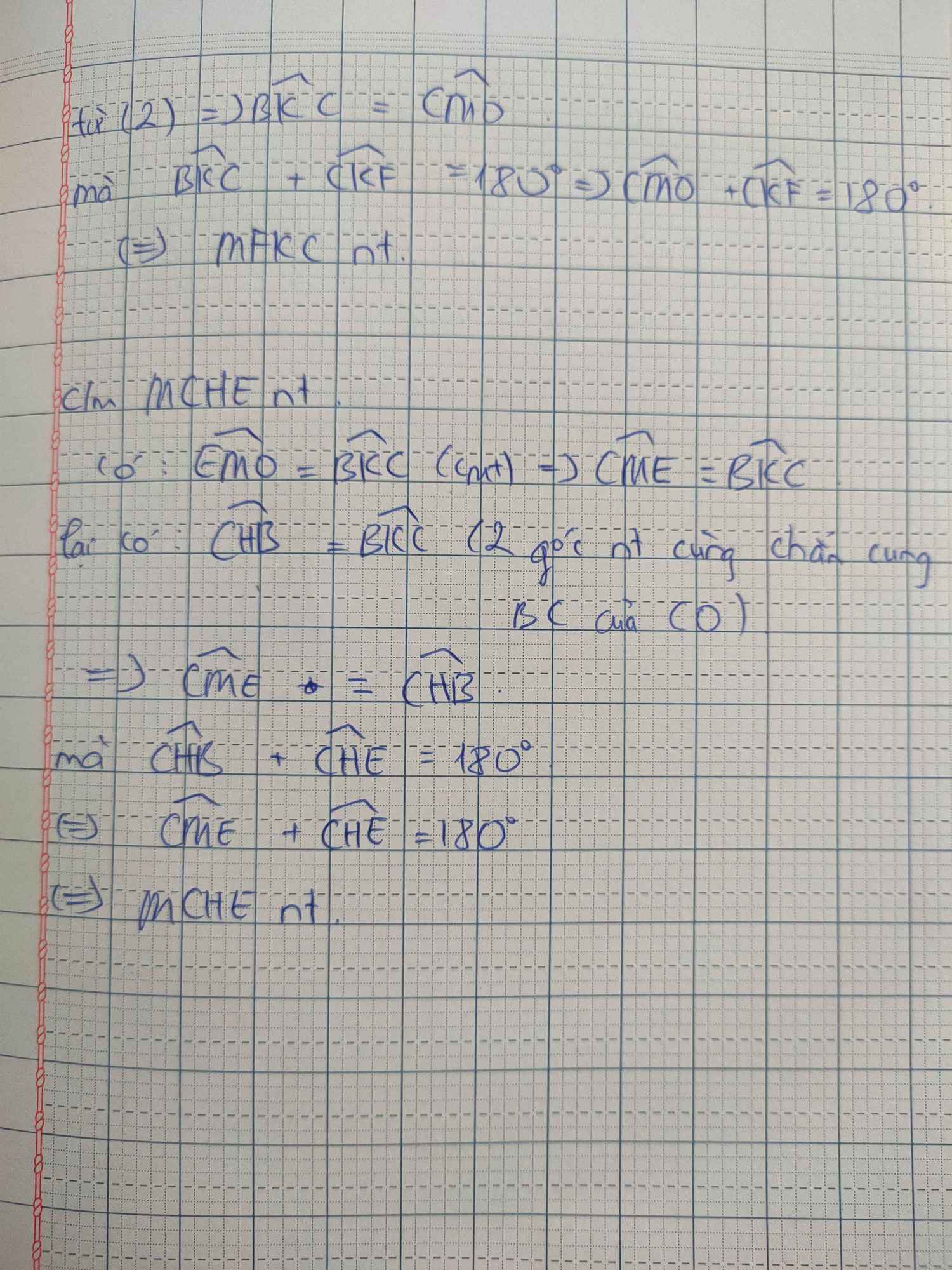
Đúng(0)
DT
Đỗ Tuệ Lâm
4 tháng 2 2022

Đúng(0)
Những câu hỏi liên quan

1 tháng 8 2023
a: Xét ΔMCD và ΔMEC có
góc MCD=góc MEC
góc CMD chung
=>ΔMCD đồng dạng với ΔMEC
b: Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại K
ΔMCO vuông tại C có CK là đường cao
nên MK*MO=MC^2
c: góc AOC=2*góc AIC=120 độ
=>góc AOM=góc COM=60 độ
Xét ΔCOM vuông tại C có tan COM=CM/CO
=>CM/R=căn 3
=>CM=R*căn 3