Cho tam giác ABC đều, gọi O là trung điểm của BC, các điểm D,E lần lượt di động trên các cạnh AB, AC, va goc DOE = 60.
a] c/m BD.CE không đổi
b] C/m DO la tia tiep phan giac cua goc BDE
c]Dung (O) tiep xux AB. C/m duong trong tiep xua voi DE va AC
d) Gọi P,Q lần lượt là tiếp điểm của (O) với AB, AC. I, N lần lượt là giao điểm của PQ với OD và OE.C/m DE+2IN

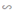 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.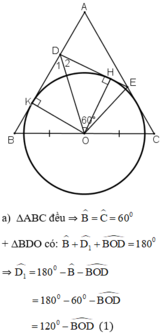
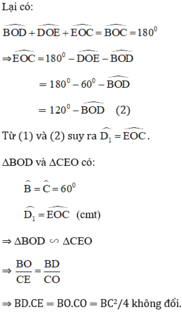
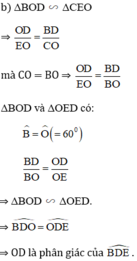
 ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
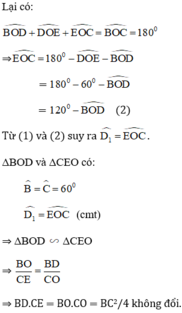
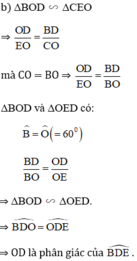
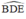
a, ^BOD + ^OBD = 120 = ^BOD + ^EOC (vì ^DOE = 60)
=> ^BDO = ^EOC
=> ∆BDO đồng dạng ∆COE
=> BD/BO = CO/CE
<=> BD.CE = BC²/4
b, DO/OE = BD/CO
<=> BO/OE = BD/OD
=> ∆BOD đồng dạng ∆OED
=> ^BDO = ^ODE
=> OD là tia phân giác của góc BDE
c, kẻ OI,OK lần lượt vuông góc với AB,DE
AB tiếp xúc với (O;OI)
có ∆IOD = ∆KOD (cạnh huyền góc nhọn)
=> OI = OK
mà OK ┴ DE
=> (O) luôn tiếp xúc với DE