Cho tam giác ABC cân tại A và M là Trung điểm của cạnh BC.Kẻ MH và MK lần lượt vuông góc với AB và AC(H thuộc AB,K thuộc AC)
a)Chứng Minh:Tam giác MBH bằng tam giác MCK
b)Cho BC=8cm và H=3cm.Tính MK
c)Chứng Minh:HK song song với BC
d)Cho HK=1/2BC.Khi đó tam giác ABC là tam giác gì vì sao

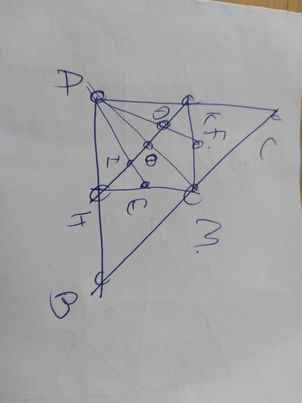
a) - Xét tam giác MHC và tam giác MKB có :
BM=AC ( Do M là trung điểm BC )
Góc BMK= Góc HMC ( đối đỉnh )
MK=MC( theo giả thiết )
=) Tam giác MHC = tam giác MKB (c.g.c)
=) Góc HKB = góc MHC=90 độ ( 2 góc tương ứng )
b) - Có KH vuông góc AC
AB vuông góc AC
=) AB//KH ( đpcm )
=) góc MAH=góc BMA và góc BMA=góc MBK ( So le trong )
=) Góc MAH=góc MBK
- Xét tam giác MKB và tam giác MHA có
Góc MBK=góc MAH(chứng minh trên)
Góc BKM= góc MHA = 90 độ
MH=MK( theo giả thiết )
=) tam giác MKB=tam giác MHA ( cạnh góc vuông-góc nhọn)
=)BK=AH ( 2 cạnh tương ứng )
* Có thể chứng minh theo cách đoạn chắn nữa(Nhiều cách lắm)
c) - Vì tam giác MHC= tam giác MKB ( chứng minh a )
=) BK=HC( 2 cạnh tương ứng)
Mà BK=AN ( chứng minh b0
=) HC=AN =) H là trung điểm AC
=) MH là đường trung tuyến của tam giác MAC mà MH đồng thời là đường cao của tam giác MAC
=) Tam giác MAC cân tại M.
d) - Có M là trung điểm BC =) AM là đường trung tuyến BC mà BH cũng là đường trung tuyến AC(chứng minh trên)
và BH cắt AM ở G =) G là trọng tâm của tam giác ABC( giao 3 đường trung tuyến )
=) AG = 1/3 AM (1)
Lại xét tam giác BGC có : GB+GC > BC ( theo bất đẳng thức tam giác ) (2)
Lại có tam giác ABC vuông tại A mà AM là đường trung tuyến BC
=) AM = 1/2 BC (theo tính chất)
Từ (1) =) 3AG=3.1/3AM=AM = 1/2 BC
=) 3AG<BC
Mà theo (2) thì GB+GC>BC =) GB+GC>3GA =) Đpcm .