K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1

15 tháng 5 2023
=>u1+(n-1)*d=262 và u1+(n-2)*d+u1+(n-1)*d=519
=>(n-1)*d=255 và d(n-2+n-1)=505
=>(n-1)/(2n-3)=51/101
=>101n-101=102n-153
=>-n=-52
=>n=52

CM
28 tháng 4 2019
Phương pháp
Cấp số cộng ( u n ) có số hạng đầu u1 và công sai d thì số hạng thứ n là
u n = u 1 + ( n - 1 ) d
Cách giải:
Gọi 198 là số hạng thứ n của dãy.
Ta có: 198 = u 1 + ( n - 1 ) d = - 2 + ( n - 1 ) . 5
⇔ 5 n = 205 ⇔ n = 41
Chọn D.
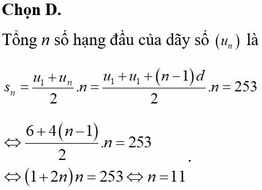


Lời giải:
Ta có:
$u_n=9-5n; u_{n+1}=9-5(n+1)$
$\Rightarrow u_{n+1}-u_n=-5$ là hằng số
Do đó $(u_n)$ là cấp số cộng với công sai $d=-5$
$u_1=9-5.1=4$
Giả sử $-9991$ là số hạng của scs nói trên.
Khi đó:
$-9991=u_k=9-5k\Rightarrow k=2000$
$\Rightarrow -9991$ là số hạng thứ $2000$
Còn $2016$ hiển nhiên không phải số hạng của csc vì $u_n=9-5n\leq 4$ với mọi $n\in\mathbb{N}\geq 1$