cho phương trình bậc 2: ax2 + bx + c = 0 thỏa mãn 2b2-9ac=0 .Chứng minh pt có 2 nghiệm và tỉ số 2 nghiệm là 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


viết lại câu hỏi khác đi, đề không rõ ràng X với x rồi . lung tung, dung công cụ soạn thảo đi nha bạn

Đặt \(f\left(x\right)=ax^{3\:}+bx^2+cx+d\left(a\ne0\right)\)
Nếu \(a< 0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)\in\left(-\infty;+\infty\right)\), với \(x\in\left(-\infty;+\infty\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm
Nếu \(a>0\) thì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\\\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm

x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0

\(Q=\dfrac{2-\dfrac{c}{a}-\dfrac{2b}{a}+\left(\dfrac{b}{a}\right)\left(\dfrac{c}{a}\right)}{1-\dfrac{b}{a}+\dfrac{c}{a}}=\dfrac{2-mn+2\left(m+n\right)-mn\left(m+n\right)}{1+m+n+mn}\)
\(Q=\dfrac{\left(2-mn\right)\left(m+n+1\right)}{\left(m+1\right)\left(n+1\right)}\ge\dfrac{\left[8-\left(m+n\right)^2\right]\left(m+n+1\right)}{\left(m+n+2\right)^2}\)
Đặt \(m+n=t\Rightarrow0\le t\le2\)
\(Q\ge\dfrac{\left(8-t^2\right)\left(t+1\right)}{\left(t+2\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{\left(2-t\right)\left(4t^2+15t+10\right)}{4\left(t+2\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(t=2\) hay \(m=n=1\)
Thầy ơi sao bên này là (2-mn) qua bên kia lại là \(\left[8-\left(m+n\right)^2\right]\) , dưới mẫu là (m+1)(n+1) qua bên này là \(\text{(m+n+2)}^2\)


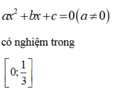
Vì 2b2 - 9ac = 0 => 9ac = 2b2 \(\ge\) 0 => tích ac \(\ge\) 0
mặt khác, 2b2 - 9ac = 0 => b2 - 4,5.ac = 0 => \(\Delta\)= b2 - 4ac = 0,5. ac \(\ge\) 0 do tích ac \(\ge\)0
=> Phương trình đã cho luôn có nghiệm
nhận xét \(\Delta\) = 0,5. ac = b2/ 9 (từ giả thiết)
Khi đó, phương trình có 2 nghiệm là
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-b+\sqrt{\frac{b^2}{9}}}{2a}=\frac{-b+\frac{\left|b\right|}{3}}{2a}=\frac{-3b+\left|b\right|}{6a}\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-b-\sqrt{\frac{b^2}{9}}}{2a}=\frac{-b-\frac{\left|b\right|}{3}}{2a}=\frac{-\left(3b+\left|b\right|\right)}{6a}\)
=> \(\frac{x_1}{x_2}=\frac{-\left(3b-\left|b\right|\right)}{-\left(3b+\left|b\right|\right)}=\frac{1}{2}\) khi b > 0 và = 2 khi b < 0
Vậy tỉ số 2 ngiệm bằng 2