cho \(\Delta\)ABC cân tại A và 2 đường trung tuyến BM,CN cắt nhau tại K
a) CM \(\Delta\)BNC = \(\Delta\)CMB
b) CM \(\Delta\)BKC cân tại K
c) CM BC < 4.KM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo tại đây nhé: https://hoc24.vn/hoi-dap/question/178224.html
Chúc bạn học tốt!

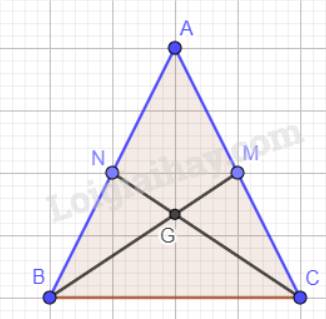
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.

a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A

a) Ta có: ΔABC cân tại A
Nên: AB=AC
Mà: CN là đường trung tuyến => NB=NA
BM là đường trung tuyến => MA=MC
Suy ra: NB=NA=MA=MC
Xét ΔBNC và ΔCMB
Có: BN=CM (cmt)
\(\widehat{B}\)=\(\widehat{C}\)(do ΔABC cân)
BC chung
Suy ra: ΔBNC=ΔCMB (c-g-c)
a)
ta có tam giác ABC cân tại A=> AB=AB=>1/2AB=1/2AC=> AN=NB=AM=MC
xét tam giác BNC và tam giác CMB có:
BC(chung)
B=C(tam gíac ABC cân tại A)
NB=MC(cmt)
suy ra tam giác BNC=CMB(c.g.c0
b)
theo câu a, ta có tam giác BNC và CMB(c.g.c)
suy ra góc NCB=MBC suy ra tam giác KCB cân tại K
c)
vì giao của 3 đường trung tuyến trong tam giác ABC là K=> K là trọng tâm của tam giác
=> MK=1/2KB mà tam giác KBC cân tại K=> 1/2KB=1/2KC
trong tam giác KBC ta có bất đẳng thức tam giác: BC<KB+KC=2KM+2KM=4KM
=>4KM>BC